Example: Sensitivity, Feasibility, and Optimization Studies
Summary—This example shows how you can achieve a design goal by using a sensitivity analysis, feasibility study, and an optimization study.
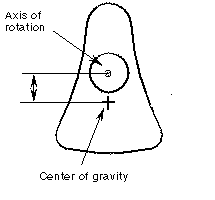
Problem—For optimal balance, the center of gravity of a crankshaft part must be coincident with its axis of rotation. The axis of rotation of the crank cannot be altered, but other design conditions, such as the width of the crank, can vary. In this part, you want to minimize the distance between the axis and the center of mass while achieving the minimum part mass.
Solution—You can find the center of gravity and create an analysis feature to measure the distance between the axis of rotation and the center of gravity. Then you can perform a sensitivity analysis to investigate which dimensions have the most effect on the location of the center of gravity. Finally, you can perform a feasibility study to investigate if it is feasible to set the distance between the center of gravity and the axis of rotation to zero. If a solution exists, you can then perform an optimization study to minimize the mass of the crank while maintaining the center of gravity on the crank axis.
1. Create an analysis feature to determine the mass properties. Click Analysis > Model > Mass Properties. Compute the mass and create a coordinate system and a datum point at the center of gravity as well as the MASS parameter.
2. Create an analysis feature to measure the distance from the datum point at the center of gravity to the axis of rotation. As a result of the measurement, create a parameter for this distance.
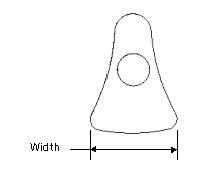
3. Perform a sensitivity analysis to determine how varying the width dimension affects the location of the center of gravity.
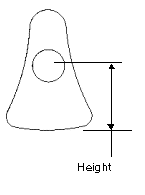
4. Perform a sensitivity analysis to determine how varying the height dimension affects the location of the center of gravity.
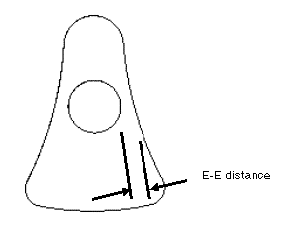
5. Create an analysis feature to measure the distance between the shaft and the outer edge of the profile of the part. You can use this measurement to define the constraints in a feasibility study. Create datum points at the beginning and end of the distance line. In the next figure, this measurement is shown as E-E distance.
6. Perform a feasibility study to determine if it is feasible to make the center of gravity coincident with the axis of rotation. In the study, you vary the width, height, and radius dimensions while maintaining some distance between the shaft of the part and the outer edge of the profile of the part (E-E distance).
7. Perform an optimization study to minimize the mass (goal function) while maintaining the same constraints as outlined in Step 6.