Creo Simulation Live - 静态结构分析验证案例

问题说明：端面之一有一个固定圆孔的矩形板，并且在对立面施加拉伸压力载荷。找到孔的圆柱面上 X 方向的最大法向应力。

J. E. Shigley, Mechanical Engineering Design, McGraw-Hill, 1st Edition, 1986, Table A-23, Figure A-23-1, pg. 673

材料属性	几何属性	负载
杨氏模量 E = 1000 帕泊松比 ν = 0.0	长度 = 15 米宽度 = 5 米厚度 = 1 米孔半径 = 0.5 米	压力 = -100 帕

结果比较 - 仿真质量滑块在默认位置

结果	目标	Creo Simulate	ANSYS Discovery Live	Creo Simulation Live	错误百分比
最大法向 X 应力 (帕)	312.5	313.272	296.5	283.7	9.22

结果比较 - 仿真质量滑块在最大位置

结果	目标	Creo Simulate	ANSYS Discovery Live	Creo Simulation Live	错误百分比
最大法向 X 应力 (帕)	312.5	313.272	337.8	313.6	0.36

问题说明：考虑一个阶梯式轴，在轴的较小截面上应用轴向载荷 1000 psi，根据圆角半径计算阶梯上的应力集中，如下所示：

参考资料：Roark’s Formulas for Stress and Strain, Warren C. Young and Richard G. Budynas,2002

材料属性	几何属性	负载
杨氏模量 E = 2.9008e7 psi 泊松比 ν = 0.3	D = 8 英寸 h = 3 英寸 r = 1 英寸	压力 = -1000 psi

结果比较 - 仿真质量滑块在默认位置

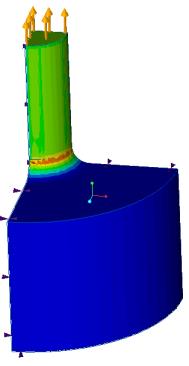
结果	目标	Creo Simulate	ANSYS Discovery Live	Creo Simulation Live	错误百分比
最大法向 Y 应力 (psi)	1376	1422.63	1497.7	1500	9.01

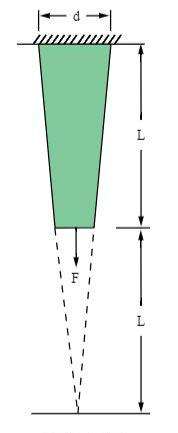
问题说明：从天花板上悬挂的方形截面和长度 l 的锥形铝合金棒材。轴向载荷 F 应用于棒材的自由端。确定棒材的最大轴向偏转 d 和中端 (Y = L/2) 的轴向应力 σy。

参考资料：C. O. Harris, Introduction to Stress Analysis, The Macmillan Co., New York, NY, 1959,pg. 237, problem 4

材料属性	几何属性	负载
杨氏模量 E = 10.4e6 psi 泊松比 ν = 0.3	长度 = 10 英寸偏离 = 2 英寸	F = 10000 lbf

结果比较 - 仿真质量滑块在默认位置

问题说明：考虑一个具有固定边的圆形板，受均匀分布的压力载荷。确定板中心处的最大偏转。

参考资料：R. J. Roark, W. C. Young,Formulas for Stress and Strain, McGraw-Hill Book Co., Inc.,New York, NY, 1975, Table 24.

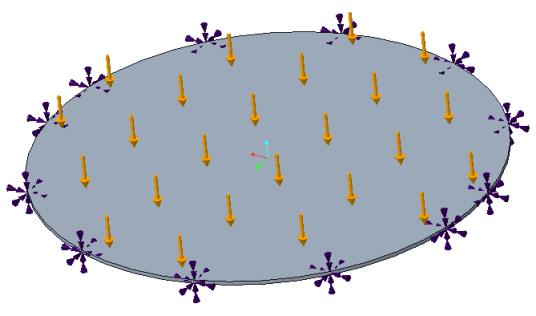
材料属性	几何属性	负载
杨氏模量 E = 30e6 psi 泊松比 ν = 0.3	直径 = 30 英寸厚度 = 0.25 英寸	P = 3 psi

结果 - 仿真质量滑块处于默认位置

结果比较 - 仿真质量滑块在最大位置 (M2000 显卡)

结果	目标	Creo Simulate	ANSYS Discovery Live	Creo Simulation Live	错误百分比
板中心处的最大偏转 (英寸)	0.0553	0.0549	0.0515	0.0515	6.87

结果比较 - 仿真质量滑块在最大位置 (P4000 显卡)

结果	目标	Creo Simulate	ANSYS Discovery Live	Creo Simulation Live	错误百分比
板中心处的最大偏转 (英寸)	0.0553	0.0549	0.0534	0.0534	3.43