Включение сквозной привязки
Поведение сквозной привязки является неустойчивым в смещении структуры. Смещение перескакивает с одной конфигурации на другую даже без увеличения внешней нагрузки.
Поведение обратной привязки является неустойчивым в смещении структуры, когда смещение перескакивает с одной конфигурации на другую даже без увеличения заданного смещения.
В большинстве нелинейных анализов используется метод ньютоновского типа (метод управления нагрузкой), чтобы найти приближенное решение для каждого шага вдоль кривой отклонения силы. Нагрузка увеличивается на конечную величину на каждом шаге и удерживается зафиксированной в процессе выполнения итераций уравновешивания. В случае сквозной привязки (контроль нагрузки) два решения могут существовать в предельной точке. При повышении нагрузки смещение может перескочить, и маловероятно, что анализ сойдется из-за величины скачка. Также и для метода контроля смещения решение может не сойтись, если случился большой скачок нагрузки.
Следующий рисунок показывает кривую смещения нагрузки для нелинейного анализа, где λ - это приложенная нагрузка, а μ - смещение.

1. o-a-d - сквозная привязка (при управлении нагрузкой)
2. o-a-b-c - привязка снизу (при управлении смещением)
В данном примере при использовании метода управления нагрузкой анализ не сходится после точки a или пути o-a-d, предоставляя неполные или обманчивые данные о стабильности структуры. При использовании метода управления смещением анализ также может не сойтись после точки b и описать путь o-a-b-c.
В методе управления нагрузкой постоянным остается шаг изменения нагрузки, а в методе управления смещением - шаг изменения смещения. Однако в алгоритме метода длины дуги коэффициент нагрузки изменяется для каждой итерации, поэтому решение идет по специфичному пути, пока не сойдется. Данный метод записывает дополнительные пары нагрузки и смещения для баланса.
Сведения о методах длины дуги в нелинейном анализе
Полное исследование путей решения нелинейной системы уравнений равновесия представляет большой практический интерес для изучения общего критического поведения структур. Методы, в которых используется общее отслеживание траектории, называют методами длины дуги. Основная идея таких методов состоит в добавлении ограничительного условия к набору нелинейных уравнений, по которому можно определить неизвестный параметр нагрузки. Поскольку методы отслеживания траектории хорошо изучены, доступна литература по большому числу различных методов. Среди множества существующих шагово-итерационных нелинейных методов решения наиболее популярным является метод длины дуги, который был разработан Риксом (1979), а затем изменен Крисфилдом (1981). В Creo Simulate используется метод длины дуги Крисфилда.
Для простых структур требуется только найти уровень нагрузки в предельной точке, когда структура неспособна выдержать дополнительную нагрузку и разрушается. Разрушающие нагрузки часто связаны с невозможностью обеспечить сходимость с помощью итерационной процедуры решения. Для других моделей может оказаться важным выполнение анализа отдельных компонентов структуры и получение информации о природе отклика после предельных точек (см. рис. 1). Это позволяет обеспечить производительность и устойчивость структуры в целом и понять поведение структуры при переходе через области нестабильности, как показано на рис. 2.

Рис. 1
1. Предельные точки
2. F - нагрузка
3. u - смещение
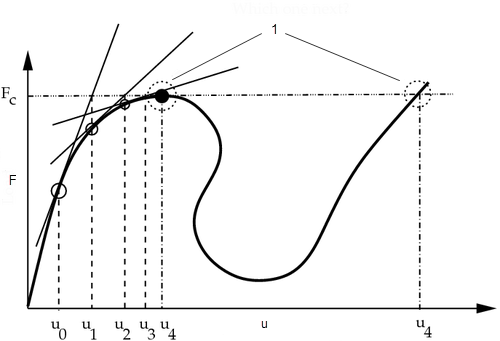
Рис. 2
1. Какая точка следующая?
2. F - нагрузка
3. u - смещение
Метод длины сферической дуги Крисфилда
Крисфилд (1981) в своем методе длины дуги использовал гиперсферу. В качестве итерационной процедуры используется этот подход в сочетании с измененным методом Ньютона - Рафсона (m.N-R). При использовании этого метода касательная матрица жесткости не переформировывается и не рефакторизуется при каждой итерации, а остается фиксированной и формируется и факторизуется только в начале каждого приращения нагрузки. На рис. 4 представлена качественная иллюстрация метода Крисфилда с m.N-R для одномерной задачи.

Рис. 4
1. Гиперсфера
2. Равновесные итерации
3. F - внешняя сила
4. u - смещение
При выборе опции Включить сквозную привязку (Include Snap-through) на вкладке Сходимость (Convergence) активируется метод длины сферической дуги Крисфилда, обеспечивающий точное отслеживание кривой нагрузка-смещение в структурах со сквозной привязкой и привязкой сзади.
Для анализа больших деформаций, если для метода сходимости выбрана опция Однопроходная адаптация (Single-Pass Adaptive) или Быстрый контроль (Quick Check), выберите опцию Включить сквозную привязку (Include Snap-through), чтобы активировать алгоритм длины дуги. После этого станет доступна история смещения для решения проблем сквозной привязки и потери устойчивости. Выбирайте эту опцию только при необходимости, поскольку она требует дополнительных вычислительных ресурсов.
Для анализа сквозной привязки или потери устойчивости модуль Creo Simulate записывает начало и конец сквозной привязки в сводный файл .rpt.
Для дополнительного исследования выходных данных можно также использовать следующие опции конфигурации.
• sim_newton_debugprint - установите для этой опции значение yes, чтобы напечатать подробную информацию отладки в файл .pas для методов mN-R и длины дуги.
• sim_nl_ldc - печать кривой нагрузка-отклонение в файл .ldc, если установлено значение yes. Файл .ldc представляет собой текстовый файл с разделенными запятыми значениями нагрузки и смещения для каждого шага времени вывода.
• sim_snap_tolerance_factor - определяет, следует ли начать или отложить сквозную привязку. Чтобы отложить сквозную привязку, установите для этой опции значение больше 1. Чтобы начать сквозную привязку раньше, установите для этой опции значение меньше 1.
Кривую нагрузка-смещение для анализа сквозной привязки или потери устойчивости можно показать, задав график зависимости смещения от приложенной нагрузки, как описано в разделе Отображение сквозной привязки в результатах.
Вернуться в раздел Опции сходимости для структурного анализа или Создание статического анализа с большой деформацией.
Рекомендации по выбору наилучшего метода для анализа
• По оценкам, которые можно найти в литературе, производительность методов длины дуги является наименее удовлетворительной при колебании структуры вдоль короткого отрезка траектории нагрузка-отклонение между состояниями устойчивого и неустойчивого равновесия. Ошибка разрушения структуры начинает обнаруживаться при сходимости методов длины дуги к предельным точкам. Теоретически жесткость структуры в таких точках стремится к нулю или бесконечности, что приводит к возникновению численных ошибок. В целом в сценариях сходимости решения к предельным точкам имеет смысл опробовать различные шаги вывода, чтобы удостовериться в том, что шаги не были случайно размещены рядом с предельными точками. Если возможно, упорядочите или увеличьте шаги вывода, чтобы избежать таких предельных точек. Для феномена привязки короткой длины доказано, что метод по умолчанию (m.N-R) является более надежным, чем методы длины дуги. В таких случаях моделирование с использованием метода по умолчанию (m.N-R) и достаточно маленьких шагов обеспечивает более высокую степень понимания.
• Использование метода длины дуги Крисфилда вместе с методом m.N-R помогает решить проблемы, связанные с горизонтальными и вертикальными касательными предельными точками. Численные эксперименты с использованием методов длины дуги очень полезны при колебании структуры вдоль длинного отрезка траектории нагрузка-отклонение между состояниями устойчивого и неустойчивого равновесия. В таких моделях очень эффективно использование скорости сходимости и шагов, выбираемых этими алгоритмами.
Выбор метода требует определенной инженерной оценки. Если оба метода не обеспечивают сходимость, может потребоваться пересмотреть модель, нагрузки или стратегию решения.
Библиография
1. E. Ricks. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Structures 15,524-551 (1979).
2. Crisfield M.A. A fast incremental/iterative solution procedure that handles snap-through. Computer and Structures, 13(1):55–62, 1981