Физика
В случае многокомпонентного потока решаются скалярные уравнения переноса для скорости, давления, температуры, турбулентности и других физических величин смеси. При наличии нескольких компонентов необходимо решить дополнительные уравнения, чтобы определить, как компоненты передаются в жидкой смеси.
Описание нескольких веществ (компонентов)
Существует несколько различных, но существенных переменных для количественного описания содержания компонента  в потоке компонентов
в потоке компонентов 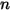 :
:
 в потоке компонентов
в потоке компонентов 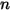 :
: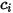 | Молярная концентрация компонента  |
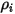 | Массовая концентрация компонента  |
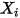 | Молярная доля компонента  |
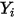 | Массовая доля компонента  |
Эти четыре величины связаны следующим образом:
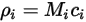
Уравнение 2.314
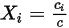
Уравнение 2.315
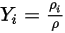
Уравнение 2.316
Здесь
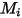 | Молекулярная масса компонента  |
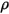 | Плотность смеси |
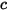 | Сумма молярных концентраций всех компонентов в системе: |
и
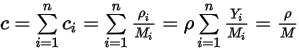
Уравнение 2.317
Здесь 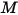 - молекулярная масса смеси:
- молекулярная масса смеси:
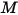 - молекулярная масса смеси:
- молекулярная масса смеси: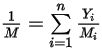
Уравнение 2.318
Уравнение 2.317 показывает, что при использовании для смеси молекулярной массы, взвешенной по массовым долям, уравнение 2.314 также применимо к смеси компонентов 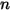 .
.
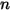 .
.Кроме того, из определений в уравнении 2.315 и уравнении 2.316 сумма как молярных, так и массовых долей должна равняться единице:
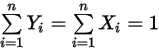
Уравнение 2.319
В CFA-решателях массовую долю произвольного компонента 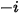 ,
,  , можно получить непосредственно, решая уравнения переноса в частных производных. Другие переменные,
, можно получить непосредственно, решая уравнения переноса в частных производных. Другие переменные, 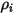 ,
, 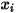 и
и 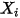 , являются вспомогательными переменными, используемыми для постобработки.
, являются вспомогательными переменными, используемыми для постобработки.
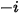 ,
,  , можно получить непосредственно, решая уравнения переноса в частных производных. Другие переменные,
, можно получить непосредственно, решая уравнения переноса в частных производных. Другие переменные, 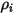 ,
, 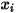 и
и 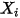 , являются вспомогательными переменными, используемыми для постобработки.
, являются вспомогательными переменными, используемыми для постобработки.Основные уравнения
В многокомпонентном потоке объемное движение смеси моделируется с помощью единых полей скорости, давления, температуры и турбулентности. Для смешивания и переноса химических веществ каждый компонент имеет собственное основное уравнение для сохранения массы. Влияние нескольких компонентов на объемный поток приводит к изменению таких свойств смеси, как плотность и вязкость, а также свойств компонентов и локальных массовых долей.
• Уравнения массовых долей
Если в потоке смеси компонентов 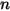 нет химических реакций, то перенос конкретного компонента
нет химических реакций, то перенос конкретного компонента  описывается следующим уравнением:
описывается следующим уравнением:
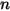 нет химических реакций, то перенос конкретного компонента
нет химических реакций, то перенос конкретного компонента  описывается следующим уравнением:
описывается следующим уравнением: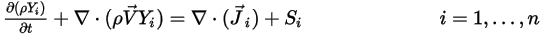
Уравнение 2.320
Здесь
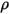 и и 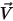 | Плотность и скорость смеси |
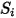 | Любой определенный пользователем источник |
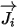 | Член массовой диффузии |
Для ламинарных потоков вектор скорости 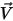 и массовая доля
и массовая доля 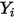 являются мгновенными переменными. Для турбулентных потоков эти векторы скорости являются осредненными по Фавру величинами, поскольку многокомпонентные потоки считаются имеющими переменную плотность, т. е. сжимаемыми.
являются мгновенными переменными. Для турбулентных потоков эти векторы скорости являются осредненными по Фавру величинами, поскольку многокомпонентные потоки считаются имеющими переменную плотность, т. е. сжимаемыми.
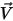 и массовая доля
и массовая доля 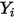 являются мгновенными переменными. Для турбулентных потоков эти векторы скорости являются осредненными по Фавру величинами, поскольку многокомпонентные потоки считаются имеющими переменную плотность, т. е. сжимаемыми.
являются мгновенными переменными. Для турбулентных потоков эти векторы скорости являются осредненными по Фавру величинами, поскольку многокомпонентные потоки считаются имеющими переменную плотность, т. е. сжимаемыми.В уравнении 2.320 значения для смеси и член массовой диффузии определяются следующим образом:
◦ Плотность смеси - усредненное по массе среднее значение для всех плотностей компонентов:
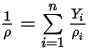
Уравнение 2.321
Для смеси газообразных веществ смешанная плотность смеси рассчитывается с помощью закона идеального газа на основании молекулярной массы смеси 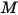 , которая вычисляется с помощью уравнения 2.318:
, которая вычисляется с помощью уравнения 2.318:
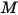 , которая вычисляется с помощью уравнения 2.318:
, которая вычисляется с помощью уравнения 2.318: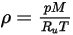
Уравнение 2.322
Здесь
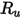 | Универсальная газовая постоянная |
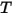 | Температура смеси |
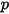 | Абсолютное давление |
Если используется рабочее давление (постоянное), уравнение 2.322 сводится к закону несжимаемого идеального газа. Это подходящее предположение для смешивания и переноса вещества, когда избыточное давление часто является незначительным по сравнению с рабочим давлением.
◦ Скорость смеси - усредненное по массе среднее значение для всех скоростей компонентов:
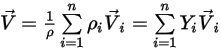
Уравнение 2.323
Однако поскольку решается только единая скорость, предполагается, что скорость смеси и все скорости компонентов имеют одинаковые значения.
◦ Поток массовой диффузии - поток массовой диффузии компонента  состоит из двух частей: ламинарного и турбулентного членов диффузии, которые выражаются следующим образом:
состоит из двух частей: ламинарного и турбулентного членов диффузии, которые выражаются следующим образом:
 состоит из двух частей: ламинарного и турбулентного членов диффузии, которые выражаются следующим образом:
состоит из двух частей: ламинарного и турбулентного членов диффузии, которые выражаются следующим образом: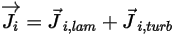
Уравнение 2.324
В уравнении 2.324 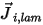 представляет ламинарный диффузионный поток компонента
представляет ламинарный диффузионный поток компонента  , который возникает из-за градиентов концентрации и температуры. По умолчанию Creo Flow Analysis использует аппроксимацию растворения или закон Фика для моделирования массовой диффузии из-за градиентов концентрации. Ламинарный диффузионный поток вычисляется по следующей формуле:
, который возникает из-за градиентов концентрации и температуры. По умолчанию Creo Flow Analysis использует аппроксимацию растворения или закон Фика для моделирования массовой диффузии из-за градиентов концентрации. Ламинарный диффузионный поток вычисляется по следующей формуле:
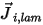 представляет ламинарный диффузионный поток компонента
представляет ламинарный диффузионный поток компонента  , который возникает из-за градиентов концентрации и температуры. По умолчанию Creo Flow Analysis использует аппроксимацию растворения или закон Фика для моделирования массовой диффузии из-за градиентов концентрации. Ламинарный диффузионный поток вычисляется по следующей формуле:
, который возникает из-за градиентов концентрации и температуры. По умолчанию Creo Flow Analysis использует аппроксимацию растворения или закон Фика для моделирования массовой диффузии из-за градиентов концентрации. Ламинарный диффузионный поток вычисляется по следующей формуле: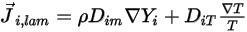
Уравнение 2.325
Здесь 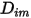 - коэффициент массовой диффузии для компонента
- коэффициент массовой диффузии для компонента  в смеси, а
в смеси, а 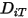 - коэффициент термодиффузии (Сорэ).
- коэффициент термодиффузии (Сорэ).
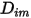 - коэффициент массовой диффузии для компонента
- коэффициент массовой диффузии для компонента  в смеси, а
в смеси, а 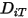 - коэффициент термодиффузии (Сорэ).
- коэффициент термодиффузии (Сорэ).Для турбулентных потоков флуктуационный член, выводящийся путем осреднения по Фавру перемешивания в уравнении 2.320, моделируется как турбулентная диффузия.
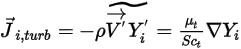
Уравнение 2.326
Здесь
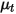 | Турбулентная вязкость |
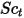 | Турбулентное число Шмидта По умолчанию: 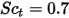 |
Турбулентная диффузии обычно существенно превышает ламинарную диффузию. Спецификация детализированных свойств ламинарной диффузии в турбулентных потоках обычно менее важна, чем турбулентный аналог.
Чтобы получить уравнение непрерывности массы для смешанного потока, добавим все уравнения для массовых долей компонентов и применим уравнение 2.319:
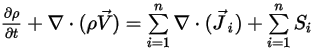
Уравнение 2.327
Чтобы удовлетворить условию общего сохранения массы в потоке смеси, сумма диффузионных членов для всех компонентов должна равняться нулю,
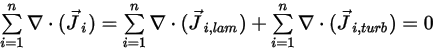
Уравнение 2.328
В уравнениях 2.319 и 2.326 член турбулентной диффузии всегда определяется с нулевым значением. Таким образом, для полностью турбулентных потоков уравнение 2.328 обычно считается выполняющимся автоматически. Однако для ламинарных потоков или при невозможности игнорировать ламинарную массовую диффузию в турбулентных потоках уравнение 2.328 сводится к следующему виду:
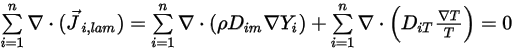
Уравнение 2.329
Затем, чтобы удовлетворить уравнение 2.329, применяются два отдельных ограничения:
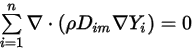
Уравнение 2.330
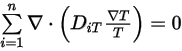
Уравнение 2.331
Уравнение непрерывности многокомпонентных потоков принимает окончательный вид:
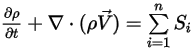
Уравнение 2.332
• Коэффициенты диффузии
Чтобы решить уравнение переноса 2.320 для многокомпонентных ламинарных потоков, требуется коэффициент массовой диффузии 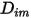 и коэффициент термодиффузии
и коэффициент термодиффузии 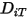 для каждого компонента в смеси. Для определения
для каждого компонента в смеси. Для определения 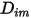 и
и 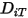 используются следующие методы:
используются следующие методы:
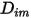 и коэффициент термодиффузии
и коэффициент термодиффузии 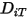 для каждого компонента в смеси. Для определения
для каждого компонента в смеси. Для определения 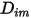 и
и 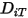 используются следующие методы:
используются следующие методы:◦ Коэффициенты массовой диффузии - формула массового диффузионного потока в ламинарных потоках, уравнение 2.325, является строго применимой, если состав смеси не изменяется или когда 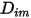 не зависит от состава. Это приемлемая аппроксимация в растворяемых смесях, когда
не зависит от состава. Это приемлемая аппроксимация в растворяемых смесях, когда 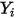 является очень малым для всех компонентов, кроме транспортирующего газа. Для нерастворяемых смесей в многокомпонентных ламинарных потоках
является очень малым для всех компонентов, кроме транспортирующего газа. Для нерастворяемых смесей в многокомпонентных ламинарных потоках 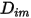 вычисляется по следующей формуле:
вычисляется по следующей формуле:
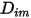 не зависит от состава. Это приемлемая аппроксимация в растворяемых смесях, когда
не зависит от состава. Это приемлемая аппроксимация в растворяемых смесях, когда 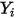 является очень малым для всех компонентов, кроме транспортирующего газа. Для нерастворяемых смесей в многокомпонентных ламинарных потоках
является очень малым для всех компонентов, кроме транспортирующего газа. Для нерастворяемых смесей в многокомпонентных ламинарных потоках 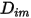 вычисляется по следующей формуле:
вычисляется по следующей формуле: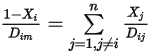
Уравнение 2.333
Здесь 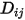 - коэффициент бинарной массовой диффузии компонента
- коэффициент бинарной массовой диффузии компонента  в компоненте
в компоненте 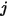 , который необходимо задать или вычислить.
, который необходимо задать или вычислить.
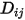 - коэффициент бинарной массовой диффузии компонента
- коэффициент бинарной массовой диффузии компонента  в компоненте
в компоненте 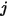 , который необходимо задать или вычислить.
, который необходимо задать или вычислить.◦ Указанное значение - коэффициент бинарной массовой диффузии 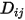 является константой или функцией температуры, если учитывается теплопередача. Можно указать значение непосредственно или получить его из указанного числа Шмидта:
является константой или функцией температуры, если учитывается теплопередача. Можно указать значение непосредственно или получить его из указанного числа Шмидта:
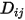 является константой или функцией температуры, если учитывается теплопередача. Можно указать значение непосредственно или получить его из указанного числа Шмидта:
является константой или функцией температуры, если учитывается теплопередача. Можно указать значение непосредственно или получить его из указанного числа Шмидта: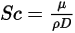
Уравнение 2.334
Здесь
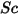 | Число Шмидта |
Число Шмидта определяется как отношение скорости вязкостной диффузии к скорости молекулярной (массовой) диффузии.
Если одно значение или одна функция температуры применяется ко всем компонентам, уравнение 2.333 сводится к
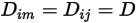
Уравнение 2.335
Уравнение 2.335 является подходящей аппроксимацией для моделирования растворяемой смеси с низкой концентрацией примесей в несущей жидкости, имеющей высокую концентрацию. В таких случаях можно определить 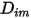 непосредственно как константу или функцию температуры.
непосредственно как константу или функцию температуры.
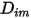 непосредственно как константу или функцию температуры.
непосредственно как константу или функцию температуры.Однако для смесей нерастворимых веществ с указанием 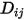 используется уравнение 2.333 для расчета отдельного коэффициента массовой диффузии в смеси
используется уравнение 2.333 для расчета отдельного коэффициента массовой диффузии в смеси  .
.
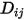 используется уравнение 2.333 для расчета отдельного коэффициента массовой диффузии в смеси
используется уравнение 2.333 для расчета отдельного коэффициента массовой диффузии в смеси  .
.◦ Кинетическая теория (Kinetic Theory) - для идеального газа двоичный коэффициент массовой диффузии 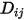 можно также получить с помощью кинетической теории.
можно также получить с помощью кинетической теории.
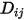 можно также получить с помощью кинетической теории.
можно также получить с помощью кинетической теории.Ссылки: H. A. McGee, "Molecular Engineering" (Молекулярная инженерия), McGraw-Hill, New York, 1991. (на английском языке)
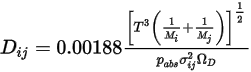
Уравнение 2.336
Здесь 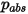 - абсолютное давление, а
- абсолютное давление, а 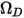 - интеграл диффузионных столкновений, который является мерой взаимодействия молекул в системе.
- интеграл диффузионных столкновений, который является мерой взаимодействия молекул в системе. 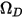 - функция количества
- функция количества 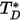 , определенного как:
, определенного как:
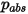 - абсолютное давление, а
- абсолютное давление, а 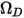 - интеграл диффузионных столкновений, который является мерой взаимодействия молекул в системе.
- интеграл диффузионных столкновений, который является мерой взаимодействия молекул в системе. 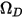 - функция количества
- функция количества 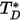 , определенного как:
, определенного как: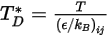
Уравнение 2.337
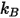 - постоянная Больцмана, которая определена как универсальная газовая постоянная
- постоянная Больцмана, которая определена как универсальная газовая постоянная 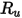 , деленная на число Авогадро.
, деленная на число Авогадро. 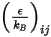 для смеси представляет геометрическое среднее:
для смеси представляет геометрическое среднее: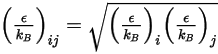
Уравнение 2.338
Для бинарной смеси 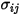 вычисляется как арифметическое среднее для отдельных
вычисляется как арифметическое среднее для отдельных 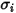 и
и 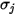 :
:
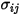 вычисляется как арифметическое среднее для отдельных
вычисляется как арифметическое среднее для отдельных 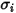 и
и 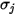 :
: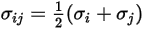
Уравнение 2.339
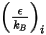 и
и 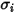 - параметры Ленарда - Джонса для компонента
- параметры Ленарда - Джонса для компонента  в смеси. В частности,
в смеси. В частности, 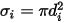 представляет сечение столкновений сферической молекулы диаметром
представляет сечение столкновений сферической молекулы диаметром 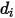 (отметим, что область столкновения молекул растягивается на двойной диаметр, так как молекула, с которой происходит столкновение, также имеет диаметр
(отметим, что область столкновения молекул растягивается на двойной диаметр, так как молекула, с которой происходит столкновение, также имеет диаметр 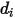 ); а
); а 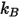 = 1.38064852(79) × 10-23 (Дж/К) - постоянная Больцмана.
= 1.38064852(79) × 10-23 (Дж/К) - постоянная Больцмана.В Creo Flow Analysis задается диаметр 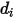 и энергия
и энергия 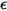 для определения двух параметров Ленарда - Джонса.
для определения двух параметров Ленарда - Джонса.
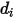 и энергия
и энергия 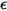 для определения двух параметров Ленарда - Джонса.
для определения двух параметров Ленарда - Джонса.◦ Коэффициенты термодиффузии 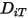 - коэффициенты термодиффузии могут быть определены как константы, полиномиальные функции температуры, пользовательские функции или с помощью следующего эмпирического выражения для зависимости от состава, которое выводится из:
- коэффициенты термодиффузии могут быть определены как константы, полиномиальные функции температуры, пользовательские функции или с помощью следующего эмпирического выражения для зависимости от состава, которое выводится из:
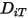 - коэффициенты термодиффузии могут быть определены как константы, полиномиальные функции температуры, пользовательские функции или с помощью следующего эмпирического выражения для зависимости от состава, которое выводится из:
- коэффициенты термодиффузии могут быть определены как константы, полиномиальные функции температуры, пользовательские функции или с помощью следующего эмпирического выражения для зависимости от состава, которое выводится из:Ссылки: K. K. Y. Kuo, “Principles of Combustion” (Принципы сжигания), John Wiley and Sons, New York, 1986. (на английском языке)
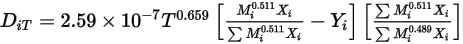
Уравнение 2.340
Эта форма коэффициента термодиффузии показывает, что тяжелые молекулы диффундируют в направлении нагретых поверхностей медленнее, а легкие молекулы - быстрее.
• Уравнения импульса
При использовании усредненных по массе свойств и скоростей уравнения импульса для смеси, в которой все компоненты имеют то же выражение, что и для одножидкостных потоков, получаем:
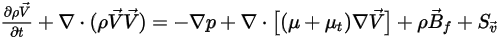
Уравнение 2.341
Здесь плотность и скорость смеси рассчитываются с помощью уравнения 2.321, уравнения 2.322 и уравнения 2.323. Турбулентная вязкость непосредственно вычисляется из моделей турбулентности на основе потока смеси, поэтому ее значение не зависит от компонентов. Ламинарная вязкость рассчитывается следующим образом:
◦ Усредненная по массе ламинарная вязкость - для смеси неидеальных газов вязкость вычисляется на основе среднего массовых долей вязкости чистых химических веществ (компонентов):
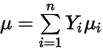
Уравнение 2.342
◦ Кинетическая теория - для смеси идеальных газов вязкость вычисляется на основе кинетической теории. Для каждого компонента динамическая вязкость рассчитывается на основе уравнения Больцмана:
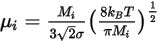
Уравнение 2.343
Для коэффициента массовой диффузии, чтобы рассчитать вязкость компонентов газа в смеси, необходимо указать параметры Ленарда - Джонса: 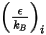 и
и 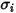 .
.
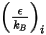 и
и 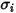 .
.Вязкость для смеси идеальных газов вычисляется следующим образом:
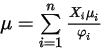
Уравнение 2.344
Здесь
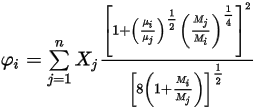
Уравнение 2.345
• Уравнение энергии
Как описано в модуле Теплота (Heat), уравнение энергии для смеси всех компонентов выражается следующим образом:
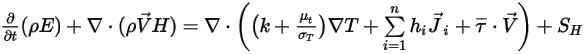
Уравнение 2.345
Здесь 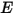 и
и 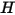 представляют общую внутреннюю энергию и общую энтальпию в смеси компонентов
представляют общую внутреннюю энергию и общую энтальпию в смеси компонентов 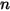 . Вместе с удельной теплоемкостью смеси
. Вместе с удельной теплоемкостью смеси 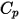 и статической энтальпией
и статической энтальпией 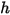 они получаются путем усреднения по массе соответствующих значений каждого компонента:
они получаются путем усреднения по массе соответствующих значений каждого компонента:
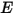 и
и 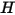 представляют общую внутреннюю энергию и общую энтальпию в смеси компонентов
представляют общую внутреннюю энергию и общую энтальпию в смеси компонентов 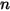 . Вместе с удельной теплоемкостью смеси
. Вместе с удельной теплоемкостью смеси 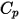 и статической энтальпией
и статической энтальпией 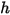 они получаются путем усреднения по массе соответствующих значений каждого компонента:
они получаются путем усреднения по массе соответствующих значений каждого компонента:◦ Усредненная по массе теплоемкость смеси
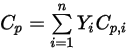
Уравнение 2.347
◦ Усредненная по массе энергия смеси и энтальпия:
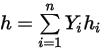
Уравнение 2.348
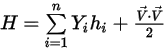
Уравнение 2.349
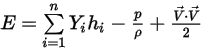
Уравнение 2.350
Статическая энтальпия компонента состоит из двух частей: эталонной энтальпии стандартного состояния и удельной энтальпии. При расчете многокомпонентных потоков включаются обе части энтальпии (абсолютное или общее значение) 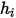 .
.
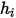 .
.В уравнении 2.336 первый член в правой части представляет рассеяние энергии. Он состоит из трех частей: теплопроводности, переноса энергии путем диффузии веществ и вязкостного нагрева. Теплопроводность смеси моделируется так же, как и в потоке единичной жидкости. В Creo Flow Analysis теплопроводность смеси рассчитывается следующим образом:
◦ Усредненная по массе теплопроводность - для смеси неидеальных газов теплопроводность рассчитывается на основе простой средней массовой доли теплопроводности чистых веществ или компонентов:
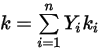
Уравнение 2.351
Это метод по умолчанию в Creo Flow Analysis.
◦ Кинетическая теория - для смеси идеальных газов теплопроводность можно рассчитать на основе кинетической теории. Для каждого компонента теплопроводность имеет вид:
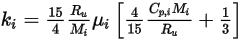
Уравнение 2.352
Здесь
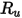 | Универсальная газовая постоянная |
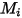 | Молекулярная масса |
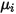 | Указанная или рассчитанная вязкость компонента |
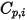 | Указанная или рассчитанная удельная теплопроводность компонента |
Отметим, что, как и ламинарную вязкость 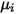 , удельную теплоемкость
, удельную теплоемкость 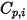 можно тоже получить с помощью кинетической теории:
можно тоже получить с помощью кинетической теории:
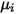 , удельную теплоемкость
, удельную теплоемкость 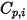 можно тоже получить с помощью кинетической теории:
можно тоже получить с помощью кинетической теории: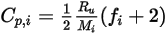
Уравнение 2.353
Здесь 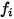 - число мод сохранения энергии (степени свободы) для компонента газа
- число мод сохранения энергии (степени свободы) для компонента газа  .
.
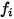 - число мод сохранения энергии (степени свободы) для компонента газа
- число мод сохранения энергии (степени свободы) для компонента газа  .
.Вязкость для смеси идеальных газов вычисляется следующим образом:
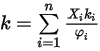
Уравнение 2.354
Здесь 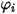 выражено в уравнении 2.335.
выражено в уравнении 2.335.
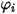 выражено в уравнении 2.335.
выражено в уравнении 2.335.Второй член диффузии,

Уравнение 2.355
Представляет перенос энтальпии путем диффузии химических веществ в потоке компонентов 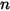 . Этот член может существенно повлиять на поле энтальпии и не должен игнорироваться. В случае числа Левиса отношение коэффициента термодиффузии
. Этот член может существенно повлиять на поле энтальпии и не должен игнорироваться. В случае числа Левиса отношение коэффициента термодиффузии 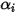 к коэффициенту массовой диффузии
к коэффициенту массовой диффузии 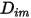 равно:
равно:
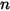 . Этот член может существенно повлиять на поле энтальпии и не должен игнорироваться. В случае числа Левиса отношение коэффициента термодиффузии
. Этот член может существенно повлиять на поле энтальпии и не должен игнорироваться. В случае числа Левиса отношение коэффициента термодиффузии 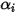 к коэффициенту массовой диффузии
к коэффициенту массовой диффузии 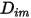 равно:
равно: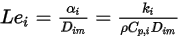
Уравнение 2.356
Для любого вещества оно не равно единице, поэтому пренебрежение этим членом может привести к серьезным ошибкам.
Третьим членом диффузии является вклад вязкостного нагрева 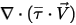 . Хотя он обрабатывается так же, как и в потоке одной жидкости, напряжение сдвига рассчитывается
. Хотя он обрабатывается так же, как и в потоке одной жидкости, напряжение сдвига рассчитывается 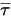 с помощью ламинарной и турбулентной вязкости. Основной член источника
с помощью ламинарной и турбулентной вязкости. Основной член источника 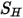 представляет полный внешний или заданный пользователем источник тепла для всех компонентов.
представляет полный внешний или заданный пользователем источник тепла для всех компонентов.
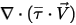 . Хотя он обрабатывается так же, как и в потоке одной жидкости, напряжение сдвига рассчитывается
. Хотя он обрабатывается так же, как и в потоке одной жидкости, напряжение сдвига рассчитывается 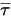 с помощью ламинарной и турбулентной вязкости. Основной член источника
с помощью ламинарной и турбулентной вязкости. Основной член источника 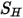 представляет полный внешний или заданный пользователем источник тепла для всех компонентов.
представляет полный внешний или заданный пользователем источник тепла для всех компонентов.• Модели турбулентности - для плотности смеси 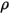 уравнения моделирования турбулентности для молекулярной вязкости
уравнения моделирования турбулентности для молекулярной вязкости 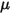 и скорости
и скорости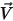 в стандартной модели k-ε и модели RNG k-ε имеют тот же общий вид, как и в моделях турбулентности одной жидкости. Они описаны в модуле Турбуленция (Turbulence). Турбулентная вязкость смеси
в стандартной модели k-ε и модели RNG k-ε имеют тот же общий вид, как и в моделях турбулентности одной жидкости. Они описаны в модуле Турбуленция (Turbulence). Турбулентная вязкость смеси 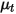 рассчитывается непосредственно из выражения:
рассчитывается непосредственно из выражения:
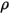 уравнения моделирования турбулентности для молекулярной вязкости
уравнения моделирования турбулентности для молекулярной вязкости 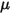 и скорости
и скорости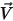 в стандартной модели k-ε и модели RNG k-ε имеют тот же общий вид, как и в моделях турбулентности одной жидкости. Они описаны в модуле Турбуленция (Turbulence). Турбулентная вязкость смеси
в стандартной модели k-ε и модели RNG k-ε имеют тот же общий вид, как и в моделях турбулентности одной жидкости. Они описаны в модуле Турбуленция (Turbulence). Турбулентная вязкость смеси 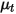 рассчитывается непосредственно из выражения:
рассчитывается непосредственно из выражения: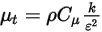
Уравнение 2.357
Кроме того, генерация турбулентной кинетической энергии рассчитывается на основе турбулентной вязкости смеси и градиентов скоростей:
Моделирование границ в многокомпонентном потоке
В многокомпонентном потоке граничные условия для уравнений потока, энергии и моделирования турбулентности совпадают с уравнениями для однофазных потоков, описанными в модулях Поток (Flow), Теплота (Heat) и Турбуленция (Turbulence). Для массовых долей компонентов граничные условия состоят из указанного значения, заданного объемного потока и/или градиента.
• Входная граница для n компонентов
Во входной границе общий перенос компонента может состоять из вкладов конвекции и диффузии. Конвекция определяется указанными для входа массовыми долями. Диффузия зависит от градиента рассчитанного поля массовых долей. При очень малых конвективных скоростях на входе может быть получена или потеряна существенная масса по причине диффузии во входном отверстии. По этой причине диффузия во входном отверстии не включается по умолчанию, но может быть включена как опция.
◦ Указанное значение - для потока компонентов 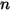 массовые доли заранее задаются для компонентов
массовые доли заранее задаются для компонентов 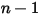 , тогда как массовая доля компонента
, тогда как массовая доля компонента 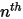 получается с помощью физического ограничения - уравнение 2.319:
получается с помощью физического ограничения - уравнение 2.319:
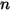 массовые доли заранее задаются для компонентов
массовые доли заранее задаются для компонентов 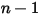 , тогда как массовая доля компонента
, тогда как массовая доля компонента 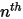 получается с помощью физического ограничения - уравнение 2.319:
получается с помощью физического ограничения - уравнение 2.319:
Уравнение 2.358
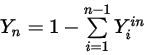
Уравнение 2.359
Кроме того, массовая доля каждого компонента должна быть неотрицательной.
◦ Указанный объемный поток - в предположении, что 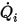 представляет заданный объемный поток во входном отверстии для компонента
представляет заданный объемный поток во входном отверстии для компонента  , имеем массовый поток каждого компонента
, имеем массовый поток каждого компонента 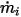 и общий массовый поток во входном отверстии
и общий массовый поток во входном отверстии 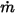 в виде:
в виде:
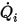 представляет заданный объемный поток во входном отверстии для компонента
представляет заданный объемный поток во входном отверстии для компонента  , имеем массовый поток каждого компонента
, имеем массовый поток каждого компонента 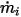 и общий массовый поток во входном отверстии
и общий массовый поток во входном отверстии 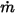 в виде:
в виде:
Уравнение 2.360
Здесь 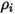 - это плотность компонента на входном отверстии
- это плотность компонента на входном отверстии  .
.
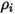 - это плотность компонента на входном отверстии
- это плотность компонента на входном отверстии  .
.По определению массовая доля вычисляется следующим образом:
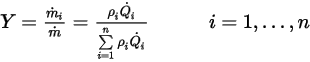
Уравнение 2.361
◦ Граница выходного отверстия, симметричная и стеночная границы - для компонентов 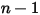 условия нулевого градиента применяются для всех границ выходных отверстий, симметричных и стеночных границ, в то время как фаза
условия нулевого градиента применяются для всех границ выходных отверстий, симметричных и стеночных границ, в то время как фаза 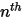 получается с использованием физического ограничения:
получается с использованием физического ограничения:
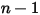 условия нулевого градиента применяются для всех границ выходных отверстий, симметричных и стеночных границ, в то время как фаза
условия нулевого градиента применяются для всех границ выходных отверстий, симметричных и стеночных границ, в то время как фаза 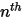 получается с использованием физического ограничения:
получается с использованием физического ограничения: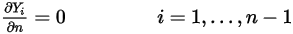
Уравнение 2.362
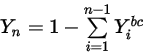
Уравнение 2.363
Здесь 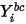 - значение границы, полученное из уравнения 2.347.
- значение границы, полученное из уравнения 2.347.
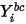 - значение границы, полученное из уравнения 2.347.
- значение границы, полученное из уравнения 2.347.Обсуждение численных расчетов
Перечисленные выше основные уравнения, модели турбулентности и граничные условия образуют основу многокомпонентной модели смешивания. Без членов внешних или заданных пользователем источников и химических реакций они представляют замкнутую систему уравнений, которая решается численно с помощью решателя для конечного объема на основе давления.
Уравнения переноса массовой доли решаются для всех компонентов. Чтобы удовлетворить физическому ограничению, фактические массовые доли масштабируются с использованием суммарного значения решений для всех компонентов:

Уравнение 2.364
Здесь 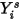 - значение, полученное из решения уравнения 2.320. Фактическая массовая доля:
- значение, полученное из решения уравнения 2.320. Фактическая массовая доля:
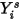 - значение, полученное из решения уравнения 2.320. Фактическая массовая доля:
- значение, полученное из решения уравнения 2.320. Фактическая массовая доля: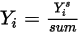
Уравнение 2.365