Heat Transfer (Перенос теплоты) (на английском языке)
Ламинарный поток через трубу с однородным тепловым потоком
Формулировка задачи: трехмерный ламинарный поток с теплопередачей моделируется в трубе с помощью модуля "Теплота" (Heat). Жидкость входит в трубу с температурой 300 К и нагревается однородным тепловым потоком на стенке трубы.
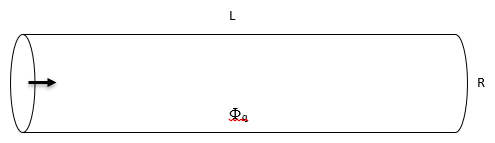
à - полностью установившийся профиль скорости при 300 К
Ссылки: F.M. White. Fluid Mechanics (Механика жидкости). 3rd Edition. McGraw Hill Book Co. Inc., New York, NY, 1994.
Свойства жидкости | Геометрические свойства | Рабочие условия |
|---|---|---|
Плотность = 13529 кг/м3 Вязкость = 0.001523 Па-с Удельная теплоемкость = 139.3 Дж/кг-К Теплопроводность = 8.54 Вт/м-К | R = 0.0025 м L = 0.1 м | Вход: полностью установившийся профиль скорости при 300 К Выход = 101325 Па Փq = 5000 Вт/м2 |
Сравнение результатов - падение давления и температура на выходе
Результаты | Аналитика | Анализ потока Creo | Ошибка в процентах |
|---|---|---|---|
Падение давления (Па) | 1 | 1.0054 | 0.54 |
Температура на выходе (К) | 340 | 340.894 | 0.26 |
Естественная конвекция в концентрическом кольцевом зазоре
Формулировка задачи: естественная конвекция моделируется в концентрическом кольцевом зазоре с помощью модуля "Теплота" (Heat). Температура внутренней стенки концентрического кольцевого зазора на 50 К выше внешней стенки.
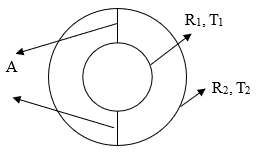
A = плоскость симметрии
Ссылки: T.H. Kuehn, R.J. Goldstein, "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli" (Экспериментальное исследование естественного конвекционного теплопереноса в концентрических и эксцентрических горизонтальных цилиндрических кольцевых зазорах", Journal of Heat Transfer, Vol 100, стр. 635-640, 1978.
Свойства жидкости | Геометрические свойства | Рабочие условия |
|---|---|---|
Плотность = идеальный газ или воздух Вязкость = 3.54822 x 10-5 Па-с | Аэродинамический профиль РАЕ 2822 AoA = 2.31 град Высота аэродинамической трубы = 72 м Длина аэродинамической трубы = 96 м | R1 = 0.0178 м T1 = 373 R2 = 0.04628 м T2 = 327 |
Результат - контуры температуры
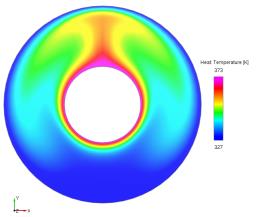
Сравнение результатов - распределение температуры вдоль симметричной стенки
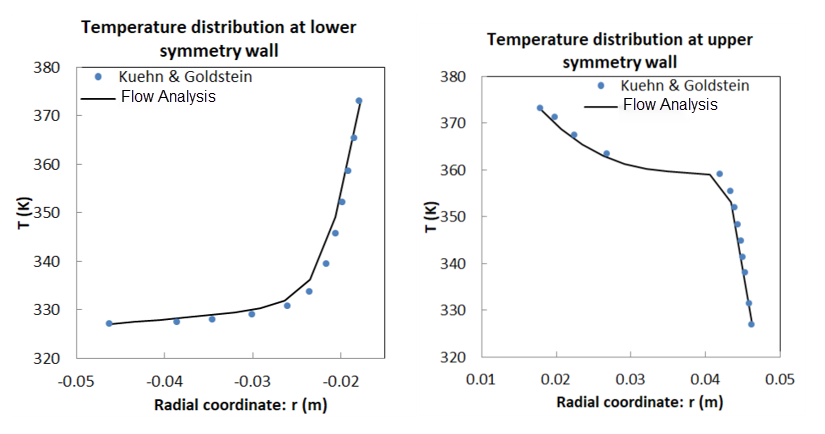
Сравнение результатов - сравнение с визуальным представлением температурных данных

Теплопроводность в составном твердотельном блоке
Формулировка задачи: теплоперенос моделируется в составном твердотельном блоке, состоящем из двух материалов с использованием модуля "Теплота" (Heat). Тепловой поток, заданный на правой стенке блока, нагревает систему.
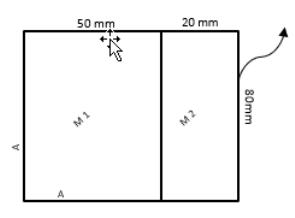
• A = адиабатная стенка
• M 1 = материал 1
◦ Плотность = 2719 кг/м3
◦ Удельная теплоемкость = 871 Дж/кг-К
◦ Теплопроводность = 75 Вт/м-К
◦ Тепловая генерация = 1.5*106Вт/м3
• M 2 = материал 2
◦ Плотность = 8978 кг/м3
◦ Удельная теплоемкость = 381 Дж/кг-К
◦ Теплопроводность = 150 Вт/м-К
References: F.P. Incropera, D.P. Dewitt.Fundamentals of Heat and Mass Transfer (Основы теплового и массового переноса). 5th Edition, стр. 117, 2006.

Сравнение результатов - распределение температуры в композитном блоке
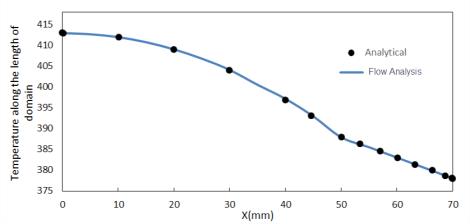
Нестационарная теплопроводность в полубесконечной плите
Формулировка задачи: полубесконечная плита нагревается в течение 120 секунд с однородным тепловым потоком на левой стенке плиты. Проводятся измерения в плите, и результаты сравниваются с аналитическим решением.
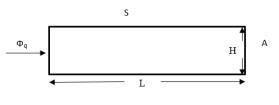
• S = симметрия
• A = адиабатная стенка
References: F.P. Incropera, D.P. Dewitt, T.L. Bergman, A.S. Lavine, Introduction to Heat Transfer (Введение в теплоперенос), 5th edition, Wiley and sons, 2007.
Свойства твердого тела | Геометрические свойства | Рабочие условия |
|---|---|---|
Плотность = 8995.64 кг/м3 Удельная теплоемкость = 381 Дж/кг-К Теплопроводность = 401 Вт/м-К | L = 0.75 м H = 0.1 м | Нестационарное = 120 с Փq = 3 x 105 Вт/м2 Начальная температура = 293 К |
Результат - контуры температуры

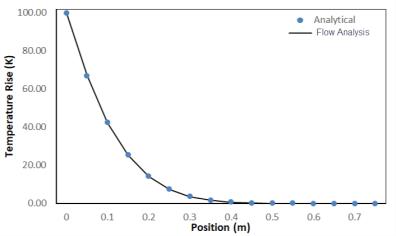
Сравнение результатов - повышение температуры в плите