Функции
Следующие функции в Редакторе выражений (Expression Editor) позволяют выполнять математические и логические операции с векторами и скалярами.
• Операторы
◦ Общие для векторов и скаляров, такие как сложение и вычитание
◦ Только скаляры, такие как квадратные корни и логарифмы
◦ Только векторы, такие как скалярные и векторные произведения
• Логические
• Тригонометрические и гиперболические
• Другие функции
• Таблицы
Операторы
Операторы позволяют выполнять математические операции с векторами и скалярами. В следующей таблице a, b, c - скаляры, а U, V, W - векторы.
|
Операторы выражений
|
Функция
|
Пример
|
|---|---|---|
|
Операторы: скаляры и/или векторы
|
||
|
Сложение
|
a = b+c или V = U+W
|
|
|
Вычитание
|
a = b-c или V = U-W
|
|
|
*
|
Умножение двух скаляров или скаляра и вектора
|
a = b*c или V = a*U (но не V = U*W)
|
|
Оператор: только скаляры
|
||
|
/
|
Деление
|
a = b/c
|
|
exp(скаляр)
|
Показательная функция с основанием e
|
a= exp(b) возводит e в степень b: a = eb
|
|
ln(скаляр)
|
натуральный логарифм с основанием e
|
a= ln(b) возвращает натуральный логарифм b
|
|
sqrt(скаляр)
|
квадратный корень
|
a = sqrt(b)
|
|
^
|
экспоненциальная функция
|
a= b^c возводит b в степень c: a = bc
|
|
Оператор: только векторы
|
||
|
&
|
скалярное произведение векторов
|
a = V&U (a = |V| |U| cos(угол))
|
|
^
|
векторное произведение
|
V=U^W (|V| = |U| |W| x sin(угол) 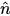 ), применяется правило правой руки. ), применяется правило правой руки. |
|
len(вектор)
|
возвращает длину вектора V
|
a = len(V)
|
|
normalize(вектор)
|
возвращает нормализованный единичный вектор V/|V|
|
V = normalize(U)
|
|
rotate(вектор,угол,направление,центр)
|
Возвращает повернутый вектор на основе угла вращения, правила правой руки, оси вращения и необязательного центра вращения. (Если центр не определен, по умолчанию используется значение 0,0,0)
|
Vrot = rotate(V,альфа,U,W), где V - вектор, который будет поворачиваться, альфа - угол в радианах, U - ось вращения. Применяется правило правой руки. W - это необязательная точка центра, определенная как вектор.
|
Логические
Логические функции позволяют включать логические операторы.
|
Операторы выражений
|
Функция
|
Пример
|
|---|---|---|
|
истина
|
логическая ИСТИНА
|
|
|
ложь
|
логическая ЛОЖЬ
|
|
|
<
|
меньше
|
|
|
>
|
больше
|
|
|
==
|
равенство при логическом сравнении
|
a = (b==3) ? 1 : 2
|
|
или
|
логическое ИЛИ
|
|
|
и
|
логическое И
|
|
|
!
|
логическое отрицание
|
!< не меньше
|
|
a = выражение ? b: c
|
a = b, если выражение имеет значение ИСТИНА;
a = c, если выражение имеет значение ЛОЖЬ
|
a = (b>3) ? 1 : 2 ==> (если b больше 3, a = 1, в противном случае a = 2)
|
Тригонометрические и гиперболические
Тригонометрические и гиперболические функции позволяют включать соответствующие функции в математические выражения.
|
Трансцендентные выражения
|
Функция
|
|---|---|
|
Тригонометрические
|
|
|
sin(радианы)
|
синус
|
|
cos(радианы)
|
косинус
|
|
cot(радианы)
|
котангенс
|
|
tan(радианы)
|
тангенс
|
|
asin()
|
обратный синус, возвращает значение в радианах
|
|
acos ()
|
обратный косинус, возвращает значение в радианах
|
|
acot()
|
обратный котангенс, возвращает значение в радианах
|
|
atan()
|
обратный тангенс, возвращает значение в радианах
|
|
atan2(y,x)
|
обратный тангенс с двумя переменными, (-пи, пи), возвращает значение в радианах
|
|
Гиперболические
|
|
|
sinh ()
|
гиперболический синус
|
|
cosh ()
|
гиперболический косинус
|
|
coth()
|
гиперболический котангенс
|
|
tanh ()
|
гиперболический тангенс
|
|
asinh()
|
обратный гиперболический синус
|
|
acosh()
|
обратный гиперболический косинус
|
|
acoth()
|
обратный гиперболический котангенс
|
|
atanh()
|
обратный гиперболический тангенс
|
Функции, связанные с отображением
Функции, связанные с отображением, относятся к панели "Отображение" (Display). Они позволяют выполнять следующие действия.
• Поддерживают создание новой переменной со всеми элементами производной переменной. Эти элементы включают возможность отображения такой функции на геометрических объектах, таких как границы и изоповерхности.
• Доступ к переменным в точках мониторинга
• Определение пользовательских переменных для графиков XY
Пользовательская переменная для 3D-отображения
display.varname - определяет пользовательские переменные, такие как контуры, изоповерхности и векторы для 3D-графиков. Новая переменная отображается на панели свойств в разделе Переменная (Variable) на вкладке Вид (View).
#display.varname: dispname [unit] - (необязательно) определяет новое наименование с единицей измерения для определяемой пользователем переменной отображения.
Например:
display.pref = flow.P - 101325
#display.pref: относительное давление [Па]
При использовании этих выражений объект относительного давления отображается под значениями свойства переменной, как показано ниже.
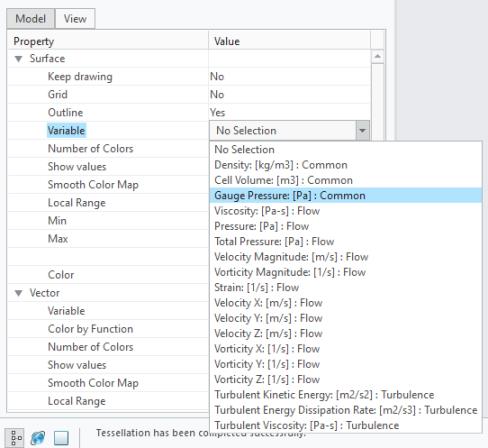
Переменные в точках мониторинга
Можно получить доступ к переменным локальных ячеек в любой точке мониторинга, используя следующий формат:
module[.subname].var@probe.name
Координаты точки:
probe.coord@probe_name
Например:
inletP = flow.P@probe."Point01"+101325
Определяемая пользователем переменная для графика XY
plot.varname - определяет пользовательскую переменную, которую можно использовать в графиках XY. Новая общая переменная добавляется как значение свойства переменной на панели свойств.
#plot.varname: dispname [unit] - (необязательно) определяет новое наименование с единицей измерения для определяемой пользователем переменной.
Например:
plot.head = (flow.pt@outlet - flow.pt@inlet)/998/9.8
#plot.head: напорная высота [м]
• Не добавляйте пробел перед символом двоеточия при определении нового наименования и единицы измерения переменной отображения или графика. • Единицы измерения по умолчанию для переменных отображения и графика отображаются в квадратных скобках. Например, для переменной давления отображается единица измерения по умолчанию "Па". При правильном определении единицы измерения она появляется на экране. В этом примере при изменении конечной отображаемой единицы измерения также преобразуются соответствующие значения. Если единица измерения не определена должным образом, программа игнорирует эту единицу измерения. |
Другие функции
Операторы выражений | Функция | Пример |
|---|---|---|
abs(x) | абсолютное значение | |
max(x,y) | максимальное значение | a = max(b,c) ==> a= b, если b >c, или a=c, если c>=b |
min(x,y) | минимальное значение | a = min(b,c) ==> a= b, если b <c, или a=c, если c<=b |
mod(x,y) | функция модуля | a = mod(c,b) ==> a = остаток деления c на b |
sgn(x) | возвращает флаг (-1, 0 или 1), указывающий знак | a= sgn(b) ==> a = -1, если b<0, или a = 0, если b=0, или a = 1, если b>0 |
step(x) | возвращает 0 или 1 в зависимости от значения относительно нуля | a = step(b) == > a = 0, если b < 0, или a = 1, если b >= 0 |
Таблицы
Табличная функция позволяет включать данные из внешних файлов таблиц, находящихся в той же папке, что и файл проекта (*.spro).
Табличные выражения | Функция |
|---|---|
table(имя_файла,x) | выполняет интерполяцию из таблицы формата 1-D |
table(имя_файла,x,y) | выполняет интерполяцию из таблицы формата 2-D |
Например:
Использование таблиц:
# Извлечение информации из таблиц
p = table("inlet_pressure.txt",time)
density = table("R134a_density.txt",temp,pre)
• Формат таблицы: 1-D (имя_файла,x) - позволяет получить доступ к одномерной таблице данных, расположенной в той же папке, что и файл проекта (*.spro).
◦ Таблица 1-D для формата равномерного распределения
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
◦ Таблица 1-D для формата неравномерного распределения
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
В формате таблицы тег outside = “flat” or outside = "extrapolation" указывает на способ определения значения, если при входном значении x y находится вне диапазона.
• Формат таблицы: 2-D (filename, x) -позволяет получить доступ к таблице данных 2-D, расположенной в той же папке, что и файл проекта (*.spro).
◦ Формат таблицы 2-D для равномерного распределения
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
◦ Формат таблицы 2-D для неравномерного распределения
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
В формате таблицы тег outside = “flat” or outside = "extrapolation" указывает, как определить значение, если при входном значении x y находится вне диапазона.
Чтобы добавить комментарий, вставьте перед текстом знак решетки (#). Не вставляйте комментарии перед XML-строкой или строкой 1. |