ウォール物理特性
ウォールの対数法則:
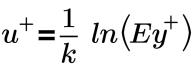
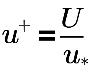
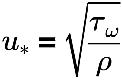
ここで、
u+ | 無次元速度 |
U | 局所 (セル中心) 速度 |
u* | 摩擦速度 |
τω | ウォールせん断 |
ρ | 流体速度 |
E | 一定係数 |
k | フォンカルマン定数 (0.41) |
y+ | ウォールからセルまでの無次元距離 |
ウォールの関数と法則
ウォール関数は、非すべり境界 (ウォール) に高密度のグリッド分布がない乱流境界レイヤーのウォール近傍の挙動をモデリングするときに必要です。文献にはさまざまなウォール関数が存在しており、特定の用途に何が適しているか調査することをお勧めします。ウォール関数の使用は Boundary Layer Theory の主題となっています (Schlichting (Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7))。
ウォールから隣接する流れのある点までの無次元の距離 y+ は以下のように定義されます。
ここで、
摩擦速度 | |
v | 動粘性 |
• 粘性サブレイヤー 0 < y+ < 5
• バッファレイヤー 5 < y+ < 30
• 慣性レイヤー 30 < y+ < 200
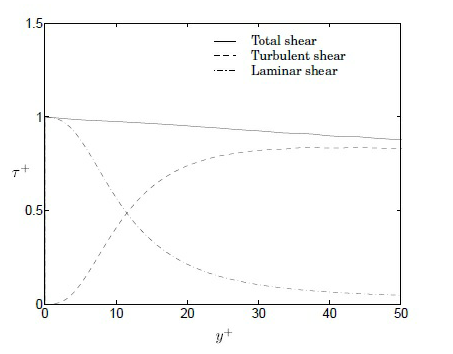
ここで説明する乱流粘性モデルをサポートするため、いくつかのウォール関数が開発されました。
• 「標準」(Standard) - Launder と Spalding によって提唱され、ウォール近傍の乱流平均速度プロファイルを定義します。「標準」(Standard) ウォール関数を使用した平均速度分布のウォールの法則は以下のように公式化されます。
慣性サブレイヤーと粘性サブレイヤー内:
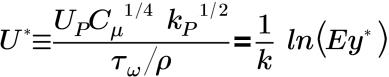
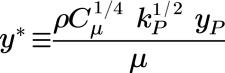
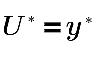
ここで、
k=0.4187 | フォンカルマン定数 |
E=9.793 | 実験定数 |
UP | 点 P における流体の平均速度 |
kP | 点 P における乱流運動エネルギー |
yP | 点 P からウォールまでの距離 |
μ | 流体の動粘度 |
「標準」(Standard) ウォール関数は工業用途で使用され、流体の流れに関するドキュメントでも説明しています。xこれは乱流運動エネルギー生成 K と乱流エネルギー散逸率の局所平衡を前提として導出されました。圧力勾配が小さく、剥離がなく、再循環がなく、加速または減速の影響がわずかである流れを予測する場合、「標準」(Standard) ウォール関数が最も正確です。
• 「Nonequilibrium(Kim)」 - Kim によって提唱され、ウォール近傍の乱流平均速度プロファイルを定義します。「Nonequilibrium(Kim)」ウォール関数を使用した平均速度分布のウォールの法則は以下のように公式化されます。
慣性サブレイヤー内:
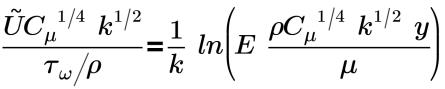
k=0.4187 | フォンカルマン定数 |
E=9.793 | 実験定数 |
UP | 点 P における流体の平均速度 |
kP | 点 P における流体の乱流運動エネルギー平均速度 |
yP | 点 P からウォールまでの距離、点 P における流体の乱流運動エネルギー平均速度 |
μ | 流体の動粘度、点 P における流体の乱流運動エネルギー平均速度 |
Cμ | 0.09 |
「Nonequilibrium(Kim)」ウォール関数は、乱流運動エネルギー生成が散逸率と等しくないことを前提としています。「Nonequilibrium(Kim)」ウォール関数では圧力勾配の影響が考慮されます。この関数では粘性サブレイヤーと完全な乱流慣性レイヤーの処理に 2 レイヤーモデルが使用されます。「Nonequilibrium(Kim)」ウォール関数では強化されたウォール処理が使用され、この処理では粘性サブレイヤー内の線形法則と慣性サブレイヤー内の対数法則の間の遷移がスムーズになるように、ウォールバッファ領域 (3 < y+ < 10) でブレンド関数が使用されます。
• 「Unified(Shih)」 - Shih によって提唱され、境界レイヤー全体での乱流平均速度プロファイルを定義します。「Unified(Shih)」ウォール関数を使用した平均速度分布のウォールの法則は以下のように公式化されます。
f1(Yτ+) および f2(Yρ+) が断片的なあてはめ関数である境界レイヤー全体:
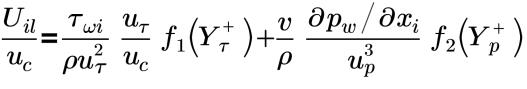
Unified (Shih) ウォール関数は、粘性サブレイヤー、バッファレイヤー、慣性サブレイヤーで有効です (統一)。Unified (Shih) ウォール関数は、順方向と逆方向の両方の圧力勾配がある流れと、加速、減速、再循環があるウォールで囲まれた複雑な流れで有効に機能します。このウォール関数では粘性サブレイヤー、バッファレイヤー、慣性レイヤーの処理に 3 レイヤーモデルが使用されます。
ウォール粗さモデル
ウォール粗さモデルは、ウォールの表面仕上げの粗さ (単位: メートル) を指します。
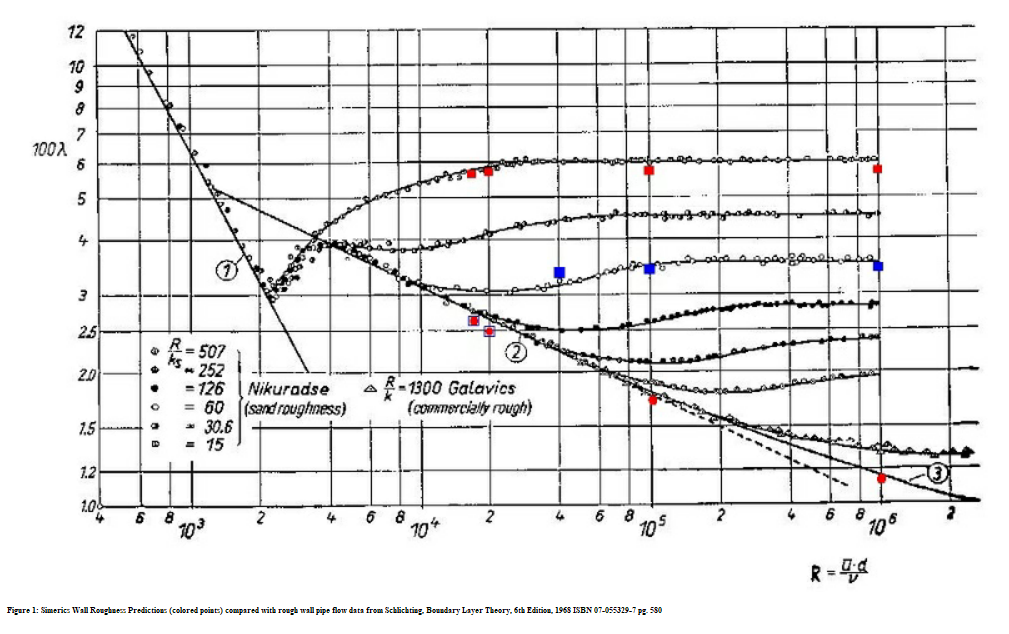
粗いウォールでのパイプフローデータと比較した Creo Flow Analysis ウォール粗さ予測 (色分けされた点) (Schlichting, Boundary Layer Theory, 6th Edition, 1968 ISBN 07-055329-7 pg. 580)。