Allgemeine Einführung: Interne Kurven
Interne Kurven definieren eine Querschnittsform einer Fläche. Zu einer durch Berandungen definierten Fläche kann eine beliebige Anzahl interner Kurven hinzugefügt werden. Dabei gelten folgende Regeln:
• Sie können keine KaF als interne Kurve hinzufügen.
• Innenkurven können aufeinander folgende (stetige) Berandungen in Berandungsflächen nicht schneiden, wie im folgenden Diagramm veranschaulicht.
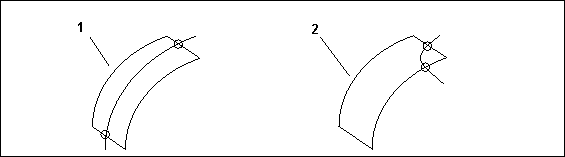
1. Richtig
2. Falsch
• Im Allgemeinen müssen interne Kurven an den Schnittstellen mit den Flächenberandungen oder anderen internen Kurven Softpoints haben (siehe folgendes Diagramm).
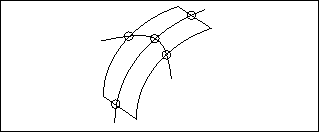
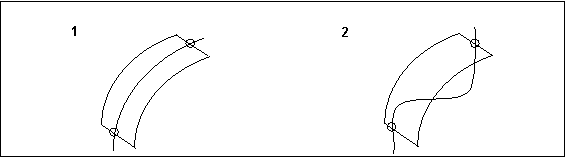
• Falls zwei Innenkurven über dieselben Ränder in einer Berandungsfläche hinausgehen, können sie sich in der Fläche nicht schneiden. Dies wird im folgenden Diagramm veranschaulicht.
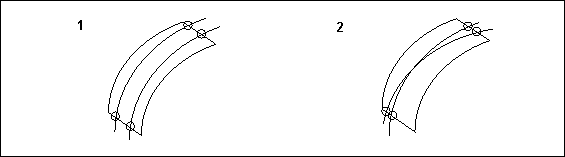
1. Richtig
2. Falsch
• Die interne Kurve muss wie im folgenden Diagramm gezeigt beide Ränder der Fläche schneiden..
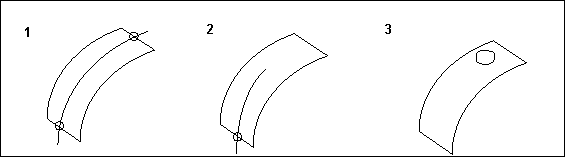
1. Richtig
2. Falsch
3. Falsch
• Eine interne Kurve kann die Flächenbegrenzung nicht an mehr als zwei Punkten schneiden.
1. Richtig
2. Falsch
• Interne Kurven auf dreieckigen Flächen müssen die natürliche Berandung nicht unbedingt schneiden.
◦ Eine interne Kurve, welche die natürliche Berandung schneidet, muss durch den fehlerhaften Eckpunkt verlaufen.
◦ Eine interne Kurve, welche die natürliche Berandung nicht schneidet, muss die beiden anderen Berandungen schneiden.