Funktionen
Die folgenden Funktionen im Ausdrucks-Editor (Expression Editor) ermöglichen die mathematische und logische Bearbeitung von Vektoren und Skalaren:
• Operatoren
◦ Für Vektoren und Skalare, wie Addition und Subtraktion
◦ Nur für Skalare, z.B. Quadratwurzeln und Logarithmen
◦ Nur für Vektoren, wie Skalar- und Kreuzprodukte
• Logische Funktionen
• Trigonometrische und hyperbolische Funktionen
• Andere Funktionen
• Tabellen
Operatoren
Die Operatoren ermöglichen die mathematische Bearbeitung von Vektoren und Skalaren. In der folgenden Tabelle sind a, b und c Skalare, und U, V und W sind Vektoren.
|
Ausdrucksoperatoren
|
Funktion
|
Beispiel
|
|---|---|---|
|
Operatoren: Skalare und/oder Vektoren
|
||
|
Addition
|
a = b+c oder V = U+W
|
|
|
Subtraktion
|
a = b-c oder V = U-W
|
|
|
*
|
Multiplikation zweier Skalare oder eines Skalars und eines Vektors
|
a = b*c oder V = a*U (aber nicht V = U * W)
|
|
Operator: nur Skalare
|
||
|
/
|
Division
|
a = b/c
|
|
exp(Skalar)
|
Exponentialfunktion zur Basis e
|
a = exp(b) potenziert e mit b: a = eb
|
|
ln(Skalar)
|
Funktion des natürlichen Logarithmus für e
|
a = ln(b) gibt den natürlichen Logarithmus von b zurück
|
|
sqrt(Skalar)
|
Quadratwurzelfunktion
|
a = sqrt(b)
|
|
^
|
Exponentialfunktion
|
a = b^c potenziert b mit c: a = bc
|
|
Operator: nur Vektoren
|
||
|
&
|
Skalarprodukt
|
a = V&U (a = |V| |U| cos (Winkel))
|
|
^
|
Kreuzprodukt
|
V = U^W (|V| = |U| |W| x sin (Winkel) 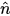 ). Die Rechte-Hand-Regel wird angewendet. ). Die Rechte-Hand-Regel wird angewendet. |
|
len(Vektor)
|
gibt die Länge des Vektors V zurück
|
a = len(V)
|
|
normalize(Vektor)
|
gibt einen normalisierten Einheitsvektor V/|V| zurück
|
V = normalize(U)
|
|
rotate(Vektor,Winkel,Richtung,Zentrum)
|
Gibt einen rotierten Vektor basierend auf dem Rotationswinkel, RHR, der Rotationsachse und einem optionalen Rotationszentrum zurück. (Wenn kein Zentrum definiert ist, wird standardmäßig 0,0,0 verwendet.)
|
Vrot = rotate(V,alpha,U,W), wobei V der zu rotierende Vektor, alpha der Winkel in Radianten und U die Rotationsachse ist. Die Rechte-Hand-Regel wird angewendet. W ist ein optionaler Mittelpunkt, der als Vektor definiert ist.
|
Logische Funktionen
Die logischen Funktionen ermöglichen das Einschließen von logischen Aussagen.
|
Ausdrucksoperatoren
|
Funktion
|
Beispiel
|
|---|---|---|
|
true
|
Logik wahr
|
|
|
false
|
Logik falsch
|
|
|
<
|
Kleiner als
|
|
|
>
|
Größer als
|
|
|
==
|
Gleich im logischen Vergleich
|
a = (b==3) ? 1 : 2
|
|
oder
|
Logisches "oder"
|
|
|
und
|
Logisches "und"
|
|
|
!
|
Logische Negation
|
!< nicht kleiner als
|
|
a = Ausdruck ? b : c
|
a = b, wenn Ausdruck wahr ist;
a = c, wenn Ausdruck falsch ist
|
a = (b>3) ? 1 : 2 ==> (wenn b größer als 3 ist, a = 1; andernfalls a = 2)
|
Trigonometrische und hyperbolische Funktionen
Die trigonometrischen und hyperbolischen Funktionen ermöglichen den Einschluss der entsprechenden Funktionen in die mathematischen Aussagen.
|
Transzendente Ausdrücke
|
Funktion
|
|---|---|
|
Trigonometrisch
|
|
|
sin(Radianten)
|
Sinusfunktion
|
|
cos(Radianten)
|
Kosinusfunktion
|
|
cot(Radianten)
|
Kotangensfunktion
|
|
tan(Radianten)
|
Tangensfunktion
|
|
asin()
|
Umkehrfunktion der Sinusfunktion, gibt den Wert in rad zurück
|
|
acos()
|
Umkehrfunktion der Kosinusfunktion, gibt den Wert in rad zurück
|
|
acot()
|
Umkehrfunktion der Kotangensfunktion, gibt den Wert in rad zurück
|
|
atan()
|
Umkehrfunktion der Tangensfunktion, gibt den Wert in rad zurück
|
|
atan2(y,x)
|
Umkehrfunktion der Tangensfunktion mit zwei Variablen, (-pi, pi), gibt den Wert in rad zurück
|
|
Hyperbolisch
|
|
|
sinh()
|
Sinus hyperbolicus
|
|
cosh()
|
Kosinus hyperbolicus
|
|
coth()
|
Kotangens hyperbolicus
|
|
tanh ()
|
Tangens hyperbolicus
|
|
asinh()
|
Umkehrfunktion des Sinus hyperbolicus
|
|
acosh()
|
Umkehrfunktion des Kosinus hyperbolicus
|
|
acoth()
|
Umkehrfunktion des Kotangens hyperbolicus
|
|
atanh()
|
Umkehrfunktion des Tangens hyperbolicus
|
Anzeigespezifische Funktionen
Anzeigespezifische Funktionen beziehen sich auf den Anzeigebereich. Sie ermöglichen Folgendes:
• Erzeugen einer neuen Variable mit allen Charakteristiken einer abgeleiteten Variable. Dazu zählt die Möglichkeit, Funktionen auf geometrischen Objekten wie Randbedingungen und Isoflächen anzuzeigen.
• Zugriff auf Variablen an Überwachungspunkten
• Definieren von Benutzervariablen für XY-Plots
Benutzerdefinierte Variable für die 3D-Anzeige
display.varname – Definiert Benutzervariablen wie Konturen, Isoflächen und Vektoren für 3D-Plots. Die neue Variable wird in der Eigenschaftenkonsole auf der Registerkarte Ansicht (View) unter Variable (Variable) angezeigt.
#display.varname: dispname [unit] (optional) – Definiert einen neuen Namen mit einer Einheit für eine benutzerdefinierte Anzeigevariable.
Beispiel:
display.pref = flow.P - 101325
#display.pref: Manometerdruck [Pa]
Wenn Sie diese Ausdrücke verwenden, wird die Einheit "Manometerdruck" (Gauge Pressure) unter den Werten für die Eigenschaft "Variable" (Variable) angezeigt, wie nachfolgend abgebildet.
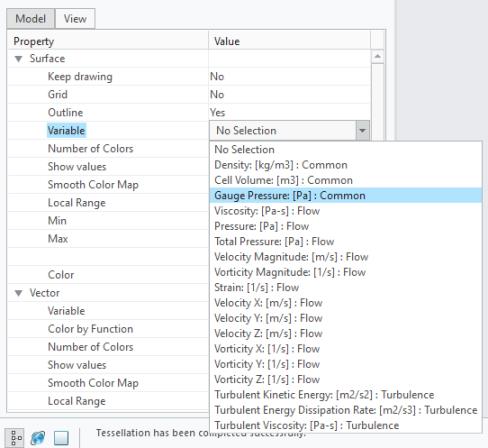
Variablen an Überwachungspunkten
Sie können an jedem Überwachungspunkt auf die lokalen Zellenvariablen zugreifen, indem Sie das folgende Format verwenden:
module[.subname].var@probe.name
Punktkoordinaten:
probe.coord@probe_name
Beispiel:
inletP = flow.P@probe."Point01"+101325
Benutzerdefinierte Variable für XY-Plot
plot.varname – Definiert eine Benutzervariable, die in XY-Plots verwendet werden kann. Die neue allgemeine Variable wird als Wert für die Eigenschaft "Variable" (Variable) in der Eigenschaftenkonsole hinzugefügt.
#plot.varname: dispname [unit] (optional) – Definiert einen neuen Namen mit Einheit für eine benutzerdefinierte Variable.
Beispiel:
plot.head = (flow.pt@outlet - flow.pt@inlet)/998/9.8
#plot.head: Druckhöhe [m]
• Fügen Sie keine Leerstelle vor dem Doppelpunkt ein, wenn Sie eine neue Ansicht oder einen Plot-Variablenamen und eine Einheit definieren. • Standardeinheiten für die Ansicht und Plotvariablen werden in eckigen Klammern angegeben. Beispiel: Die Standardeinheit Pa wird für die Druckvariable angezeigt. Wird eine Einheit ordnungsgemäß definiert, so wird sie auf dem Bildschirm angezeigt. Wenn Sie die letzte Einheit in diesem Beispiel ändern werden deren Werte ebenfalls konvertiert. Wird die Einheit nicht ordnungsgemäß definiert, so wird sie ignoriert. |
Andere Funktionen
Ausdrucksoperatoren | Funktion | Beispiel |
|---|---|---|
abs(x) | Absolutwertfunktion | |
max(x,y) | Maximumfunktion | a = max(b,c) ==> a= b wenn b >c oder a=c wenn c>=b |
min(x,y) | Minimumfunktion | a = min(b,c) ==> a= b wenn b <c oder a=c wenn c<=b |
mod(x,y) | Modulfunktion | a = mod(c,b) ==> a = der Rest von c geteilt durch b |
sgn(x) | gibt ein Flag (-1, 0 oder 1) zurück, das das Vorzeichen angibt | a = sgn(b) ==> a = -1 wenn b<0; a = 0 wenn b = 0; a = 1 wenn b>0 |
step(x) | Schrittfunktion, gibt eine 0 oder 1 zurück, je nach dem Wert relativ zu null | a = step(b) ==> a = 0 wenn b<0; a = 1 wenn b >= 0 |
Tabellen
Die Tabellenfunktion ermöglicht das Einschließen von Daten aus externen Tabellendateien, die sich im selben Verzeichnis wie die Projektdatei (*.spro) befinden.
Tabellenausdrücke | Funktion |
|---|---|
table(Dateiname,x) | interpoliert aus einer 1D-Tabelle |
table(Dateiname, x ,y) | interpoliert aus einer 2D-Tabelle |
Beispiel:
Tabellen verwenden:
# Informationen aus Tabellen extrahieren
p = table("inlet_pressure.txt",time)
Dichte = table("R134a_density.txt",temp,pre)
• Tabellenformat: 1D (Dateiname, x) – Ermöglicht Ihnen den Zugriff auf eine 1D-Datentabelle, die sich im selben Verzeichnis wie die Projektdatei (*.spro) befindet.
◦ Format der 1D-Tabelle für gleichmäßige Verteilung
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
◦ Format der 1D-Tabelle für nicht gleichmäßige Verteilung
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
Im Format legt outside = “flat” or outside = "extrapolation" unter dem table-Tag fest, wie Sie einen Wert bestimmen, wenn die Eingabe x, y außerhalb des zulässigen Bereichs liegt.
• Tabellenformat: 2D (Dateiname, x, y) – Ermöglicht Ihnen den Zugriff auf eine 2D-Datentabelle, die sich im selben Verzeichnis wie die Projektdatei (*.spro) befindet.
◦ Format der 2D-Tabelle für gleichmäßige Verteilung
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
◦ Format der 2D-Tabelle für nicht gleichmäßige Verteilung
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
Im Format legt outside = “flat” or outside = "extrapolation" unter dem table-Tag fest, wie Sie einen Wert bestimmen, wenn die Eingabe x, y außerhalb des zulässigen Bereichs liegt.
Um einen Kommentar hinzuzufügen, geben Sie vor dem Text ein Rautensymbol "#" ein. Fügen Sie keine Kommentare vor der xml-Zeile oder Zeile 1 ein. |