Physics
To create flow streamlines, the motion of massless particles is tracked based on the solved flow field, specified streamline boundary, and release conditions.
Particle Equation of Motion
To track the particle motion, the trajectory equations of each particle are solved (integrated) analytically or numerically. For a massless particle moving along with the local flow field, the motion equation is rewritten as:
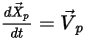
Equation 2.419
where  is the position vector of the particle; and the particle velocity
is the position vector of the particle; and the particle velocity  is the same as the flow velocity at the location
is the same as the flow velocity at the location 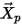 . The trajectory of
. The trajectory of 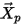 in the flow domain is then a flow streamline.
in the flow domain is then a flow streamline.
 is the position vector of the particle; and the particle velocity
is the position vector of the particle; and the particle velocity  is the same as the flow velocity at the location
is the same as the flow velocity at the location 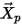 . The trajectory of
. The trajectory of 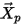 in the flow domain is then a flow streamline.
in the flow domain is then a flow streamline.Boundary Conditions
Creo Flow Analysis applies a streamline boundary condition to determine the behavior of flow streamlines at a boundary. When streamlines are at a boundary of the flow domain (including external boundaries and solid-fluid interfaces), for example a wall or an inlet boundary, one of the following can occur at the boundary:
• Streamlines are reflected.
• Streamlines enter, leave, or enter and leave through the boundary.
• Streamlines pass through an internal boundary zone, such as fan or porous jump.
Based on the streamline behavior at the boundaries, the flow boundary conditions and flow-solid interfaces are grouped again into three types of streamline boundary conditions: Open, Symmetry, Wall.
• Open—Allows streamlines to exit, enter, or exit and enter the computational domain. An open boundary is usually an inlet or outlet boundary of the fluid flow. It can also apply to the other types of flow boundaries such as wall and symmetry. At an open boundary, the streamline can leave or enter the domain depending on the particle (flow) velocity direction.
Let 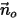 be the unit normal vector to the open boundary which points in the direction away from the computational domain. With the particle boundary velocity
be the unit normal vector to the open boundary which points in the direction away from the computational domain. With the particle boundary velocity 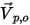 (the same as the flow velocity at the point), you have the following streamline conditions at the open boundary:
(the same as the flow velocity at the point), you have the following streamline conditions at the open boundary:
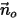 be the unit normal vector to the open boundary which points in the direction away from the computational domain. With the particle boundary velocity
be the unit normal vector to the open boundary which points in the direction away from the computational domain. With the particle boundary velocity 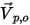 (the same as the flow velocity at the point), you have the following streamline conditions at the open boundary:
(the same as the flow velocity at the point), you have the following streamline conditions at the open boundary:◦ If 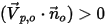 and the velocity vector
and the velocity vector  points away from the computational domain. This indicates that the particle or flow escapes through the boundary. The particle is lost from the flow domain at the point of impact with the boundary.
points away from the computational domain. This indicates that the particle or flow escapes through the boundary. The particle is lost from the flow domain at the point of impact with the boundary.
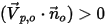 and the velocity vector
and the velocity vector  points away from the computational domain. This indicates that the particle or flow escapes through the boundary. The particle is lost from the flow domain at the point of impact with the boundary.
points away from the computational domain. This indicates that the particle or flow escapes through the boundary. The particle is lost from the flow domain at the point of impact with the boundary.◦ If  and the velocity vector
and the velocity vector 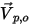 points to the computational domain. This indicates that the particle or flow enters the domain from the boundary. This particle is released or injected into the fluid flow from the open boundary, along with the inflow. The particle is a part of the streamline calculation at the point of impact with the boundary.
points to the computational domain. This indicates that the particle or flow enters the domain from the boundary. This particle is released or injected into the fluid flow from the open boundary, along with the inflow. The particle is a part of the streamline calculation at the point of impact with the boundary.
 and the velocity vector
and the velocity vector 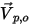 points to the computational domain. This indicates that the particle or flow enters the domain from the boundary. This particle is released or injected into the fluid flow from the open boundary, along with the inflow. The particle is a part of the streamline calculation at the point of impact with the boundary.
points to the computational domain. This indicates that the particle or flow enters the domain from the boundary. This particle is released or injected into the fluid flow from the open boundary, along with the inflow. The particle is a part of the streamline calculation at the point of impact with the boundary.• Symmetry—Streamlines are reflected at the boundary. For streamlines, a symmetry boundary typically corresponds to the flow symmetry. It can also be a location for particle release or escape in the same way as in the open streamline boundary.
Let  be the normal-to-symmetry unit vector at point
be the normal-to-symmetry unit vector at point 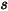 of the symmetry boundary, with its direction pointing away from the symmetry towards the computational domain. Further,
of the symmetry boundary, with its direction pointing away from the symmetry towards the computational domain. Further, 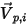 and
and 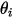 are introduced to indicate the angle of the particle impact velocity (local flow velocity) at the symmetry streamline boundary, as shown in the following figure. With the particle reflecting from the symmetry boundary, the tangential velocity remains the same while the normal velocity component only changes the sign. Mathematically, the particle or streamline symmetry boundary condition is expressed as:
are introduced to indicate the angle of the particle impact velocity (local flow velocity) at the symmetry streamline boundary, as shown in the following figure. With the particle reflecting from the symmetry boundary, the tangential velocity remains the same while the normal velocity component only changes the sign. Mathematically, the particle or streamline symmetry boundary condition is expressed as:
 be the normal-to-symmetry unit vector at point
be the normal-to-symmetry unit vector at point 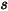 of the symmetry boundary, with its direction pointing away from the symmetry towards the computational domain. Further,
of the symmetry boundary, with its direction pointing away from the symmetry towards the computational domain. Further, 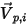 and
and 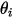 are introduced to indicate the angle of the particle impact velocity (local flow velocity) at the symmetry streamline boundary, as shown in the following figure. With the particle reflecting from the symmetry boundary, the tangential velocity remains the same while the normal velocity component only changes the sign. Mathematically, the particle or streamline symmetry boundary condition is expressed as:
are introduced to indicate the angle of the particle impact velocity (local flow velocity) at the symmetry streamline boundary, as shown in the following figure. With the particle reflecting from the symmetry boundary, the tangential velocity remains the same while the normal velocity component only changes the sign. Mathematically, the particle or streamline symmetry boundary condition is expressed as: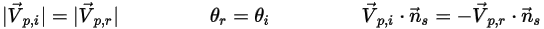
Equation 2.420
where,
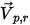 | particle reflecting velocity |
 | angle at point  of the symmetry boundary of the symmetry boundary |
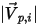 | velocity magnitude |
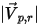 | velocity magnitude |
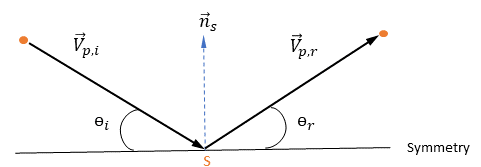
figure
Since massless particles travel at the local flow velocity, obtained by flow simulations, no boundary condition is required when you integrate equation 2.419 at a streamline symmetry boundary.
• Wall Streamline Boundary
For streamlines, a wall streamline boundary typically corresponds to the wall flow boundary. At a streamline wall boundary, the massless particles move with the fluid flow. Since the local flow velocity, thus the particle velocity, is obtained using the appropriate near-wall models, no explicit wall boundary condition is required to solve equation 2.419.
Streamline wall boundaries can be the external walls and fluid-solid interfaces. For the open and symmetry streamline boundaries, a wall streamline boundary can also be a location for particle releases.
Particle Release
The releasing particles from a specified streamline boundary provide the initial conditions and values for the streamlines. As in the Lagrange particle tracking, the procedure to determine initial conditions involves particle releases (direction, location, number of the particles and distributions) from boundaries (open, symmetry, wall and interface), and assigning properties for each particle.
For streamlines, the initial velocity of each massless particle 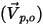 , at its release position
, at its release position 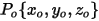 is automatically set to be the same as the local flow velocity
is automatically set to be the same as the local flow velocity 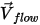 . In Creo Flow Analysis, the Release Particle options controls the release of streamline particles.
. In Creo Flow Analysis, the Release Particle options controls the release of streamline particles.
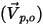 , at its release position
, at its release position 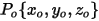 is automatically set to be the same as the local flow velocity
is automatically set to be the same as the local flow velocity 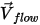 . In Creo Flow Analysis, the Release Particle options controls the release of streamline particles.
. In Creo Flow Analysis, the Release Particle options controls the release of streamline particles.Animation of Streamlines
To create and visualize the flow streamlines as curves, the trajectory equation of each particle, equation 2.419, is solved or integrated numerically. With the flow solutions, the particle or flow velocity value is known, and you calculate the particle displacement using the forward Euler integration of the particle velocity over the animation time size 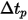 :
:
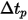 :
: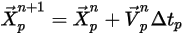
Equation 2.421
where,
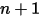 | new values |
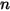 | current values |
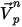 | particle (local flow) velocity |
At the first time-step, 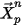 is the release position and
is the release position and  is the release velocity:
is the release velocity:
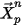 is the release position and
is the release position and  is the release velocity:
is the release velocity:
Equation 2.422
Note that the user-specified animation time-step 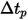 is a real number multiplier used to animate the streamlines. A value of 1 indicates that the animation curves are the same as the local velocity. The value of
is a real number multiplier used to animate the streamlines. A value of 1 indicates that the animation curves are the same as the local velocity. The value of 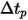 changes the curve flow speed to
changes the curve flow speed to 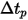 times the local flow velocity.
times the local flow velocity.
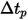 is a real number multiplier used to animate the streamlines. A value of 1 indicates that the animation curves are the same as the local velocity. The value of
is a real number multiplier used to animate the streamlines. A value of 1 indicates that the animation curves are the same as the local velocity. The value of 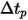 changes the curve flow speed to
changes the curve flow speed to 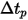 times the local flow velocity.
times the local flow velocity.Also, you can specify the diameter of the streamline curves for Line Thickness. The length of a streamline curve is equal to the local velocity multiplied by the animation time-step:  . In addition, to prevent the streamline tracking procedure from spending high amounts of computational time for tracking a streamline that is either looping or stagnant, you can introduce the user-input Maximum Integral Steps to limit how far the streamline algorithm is used to track a streamline. A small value reduces the computing time, but a very small value can end the streamline early.
. In addition, to prevent the streamline tracking procedure from spending high amounts of computational time for tracking a streamline that is either looping or stagnant, you can introduce the user-input Maximum Integral Steps to limit how far the streamline algorithm is used to track a streamline. A small value reduces the computing time, but a very small value can end the streamline early.
 . In addition, to prevent the streamline tracking procedure from spending high amounts of computational time for tracking a streamline that is either looping or stagnant, you can introduce the user-input Maximum Integral Steps to limit how far the streamline algorithm is used to track a streamline. A small value reduces the computing time, but a very small value can end the streamline early.
. In addition, to prevent the streamline tracking procedure from spending high amounts of computational time for tracking a streamline that is either looping or stagnant, you can introduce the user-input Maximum Integral Steps to limit how far the streamline algorithm is used to track a streamline. A small value reduces the computing time, but a very small value can end the streamline early.