Physics
For a multicomponent flow, you solve the scalar transport equations for mixture velocity, pressure, temperature, turbulence, and other physical quantities. When multiple components are present, you must solve additional equations to determine how the components are transported within the fluid mixture.
Description of the Multiple Species (Component)
There are several different, but related variables to quantify the content of a component  in
in 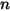 component flow:
component flow:
 in
in 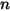 component flow:
component flow: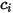 | molar concentration of component  |
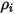 | mass concentration of component  |
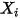 | molar fraction of component  |
 | mass fraction of component  |
The four quantities are related as follows:
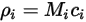
Equation 2.314
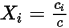
Equation 2.315
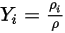
Equation 2.316
where,
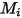 | molecular weight of component  |
 | mixture density |
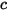 | sum of the molar concentrations of all the components in a system: |
and
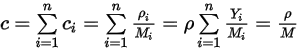
Equation 2.317
where 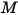 is the mixture molecular weight:
is the mixture molecular weight:
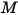 is the mixture molecular weight:
is the mixture molecular weight: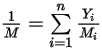
Equation 2.318
Equation 2.317 indicates that with mass-fraction weighted molecular weight for the mixture, equation 2.314 also applies to the mixture of the 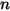 components.
components.
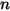 components.
components.Also, from the definitions in equation 2.315 and equation 2.316, the sum of both the molar and mass fractions must be unity:
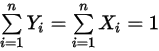
Equation 2.319
In CFA solvers, you obtain the mass fraction of the arbitrary component 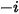 ,
, 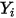 directly by solving partial differential transport equations. The other variables,
directly by solving partial differential transport equations. The other variables, 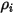 ,
, 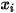 , and
, and 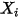 are auxiliary variables that you use for postprocessing.
are auxiliary variables that you use for postprocessing.
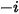 ,
, 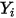 directly by solving partial differential transport equations. The other variables,
directly by solving partial differential transport equations. The other variables, 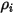 ,
, 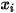 , and
, and 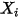 are auxiliary variables that you use for postprocessing.
are auxiliary variables that you use for postprocessing.Governing Equations
In a multicomponent flow, the bulk motion of the mixture is modeled using the single velocity, pressure, temperature, and turbulence fields. For the mixing and transport of the chemical species, each component has its own governing equation for the conservation of mass. The influence of multiple components on the bulk flow is felt through the variation of the mixture properties like density, viscosity, with the component properties and the local mass fractions.
• Mass Fraction Equations
For  component mixture flow, if there are no chemical reactions, then transport of an arbitrary component
component mixture flow, if there are no chemical reactions, then transport of an arbitrary component  is governed by the following equation:
is governed by the following equation:
 component mixture flow, if there are no chemical reactions, then transport of an arbitrary component
component mixture flow, if there are no chemical reactions, then transport of an arbitrary component  is governed by the following equation:
is governed by the following equation:
Equation 2.320
where,
 and and 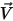 | mixture density and velocity |
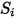 | any user-defined source |
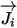 | mass diffusion term |
For laminar flows, the velocity vector 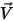 and the mass fraction
and the mass fraction 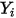 are instantaneous variables. For turbulent flows these velocity vectors are Favre-averaged quantities since multicomponent flows are considered as variable density or compressible flows.
are instantaneous variables. For turbulent flows these velocity vectors are Favre-averaged quantities since multicomponent flows are considered as variable density or compressible flows.
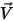 and the mass fraction
and the mass fraction 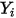 are instantaneous variables. For turbulent flows these velocity vectors are Favre-averaged quantities since multicomponent flows are considered as variable density or compressible flows.
are instantaneous variables. For turbulent flows these velocity vectors are Favre-averaged quantities since multicomponent flows are considered as variable density or compressible flows.In equation 2.320, the mixture quantities and the mass diffusion term are defined as follows:
◦ Mixture Density—Mass-averaged value of all the component densities:
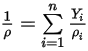
Equation 2.321
For a mixture of gaseous species, the mixture density is computed using the ideal gas law based on the mixture molecular weight 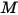 , that you calculate using equation 2.318:
, that you calculate using equation 2.318:
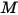 , that you calculate using equation 2.318:
, that you calculate using equation 2.318: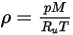
Equation 2.322
where,
 | universal gas constant |
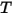 | mixture temperature |
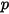 | absolute pressure |
If you use the operating pressure (constant), then equation 2.322 is reduced to the so-called incompressible ideal gas law. It is an appropriate assumption for the mixing and transport of species, where the gauge pressure is often negligible compared to the operating pressure.
◦ Mixture Velocity—Mass-averaged value of all the component velocities:

Equation 2.323
However, since only a single velocity is solved, you assume that the mixture velocity and all the component velocities have the same values.
◦ Mass Diffusion Flux—Mass diffusion flux of the component  consists of two parts: the laminar and turbulent diffusion terms, which are expressed as:
consists of two parts: the laminar and turbulent diffusion terms, which are expressed as:
 consists of two parts: the laminar and turbulent diffusion terms, which are expressed as:
consists of two parts: the laminar and turbulent diffusion terms, which are expressed as: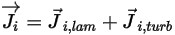
Equation 2.324
In equation 2.324, 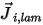 is the laminar diffusion flux of the component
is the laminar diffusion flux of the component  which arises due to gradients of concentration and temperature. By default, Creo Flow Analysis uses the dilute approximation or Fick's law to model the mass diffusion due to concentration gradients. The laminar diffusion flux has the following formulation:
which arises due to gradients of concentration and temperature. By default, Creo Flow Analysis uses the dilute approximation or Fick's law to model the mass diffusion due to concentration gradients. The laminar diffusion flux has the following formulation:
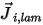 is the laminar diffusion flux of the component
is the laminar diffusion flux of the component  which arises due to gradients of concentration and temperature. By default, Creo Flow Analysis uses the dilute approximation or Fick's law to model the mass diffusion due to concentration gradients. The laminar diffusion flux has the following formulation:
which arises due to gradients of concentration and temperature. By default, Creo Flow Analysis uses the dilute approximation or Fick's law to model the mass diffusion due to concentration gradients. The laminar diffusion flux has the following formulation: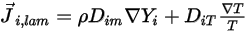
Equation 2.325
where  is the mass diffusion coefficient for the component
is the mass diffusion coefficient for the component  in the mixture; and
in the mixture; and 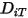 is the thermal (Soret) diffusion coefficient.
is the thermal (Soret) diffusion coefficient.
 is the mass diffusion coefficient for the component
is the mass diffusion coefficient for the component  in the mixture; and
in the mixture; and 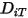 is the thermal (Soret) diffusion coefficient.
is the thermal (Soret) diffusion coefficient.For turbulent flows, the fluctuating term derived from Favre averaging the advection in equation 2.320, is modeled as turbulent diffusion:
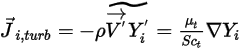
Equation 2.326
where,
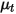 | turbulent viscosity |
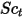 | turbulent Schmidt number 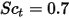 by default by default |
Turbulent diffusion generally overwhelms the laminar diffusion. Specification of detailed laminar diffusion properties in turbulent flows is generally less important than the turbulent counterpart.
To derive the mass continuity equation for the mixture flow, add all the component mass fraction equations and apply equation 2.319:
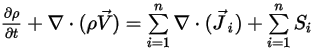
Equation 2.327
To satisfy the total mass conservation of the mixture flow, the sum of the diffusion terms for all components must be zero,
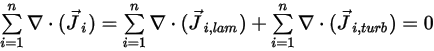
Equation 2.328
From equation 2.319 and equation 2.326, the turbulent diffusion term is always determined at zero. Therefore, for fully turbulent flows, you usually consider equation 2.328 automatically satisfied. However, for laminar flows, or when you cannot ignore the laminar mass diffusion in turbulent flows, equation 2.328 reduces to the following form:
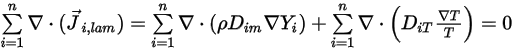
Equation 2.329
Then to satisfy equation 2.329, you apply the two separate constraints:

Equation 2.330
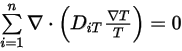
Equation 2.331
The continuity equation of the multicomponent flows then has the final form:
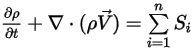
Equation 2.332
• Diffusion Coefficients
To solve the transport equation 2.320 for multicomponent laminar flows, you require the mass diffusion coefficient 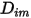 and the thermal diffusion coefficient
and the thermal diffusion coefficient 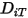 for each component in a mixture. The methods to determine
for each component in a mixture. The methods to determine  and
and 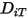 are the following:
are the following:
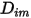 and the thermal diffusion coefficient
and the thermal diffusion coefficient 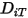 for each component in a mixture. The methods to determine
for each component in a mixture. The methods to determine  and
and 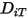 are the following:
are the following:◦ Mass Diffusion Coefficients—Formulation of the mass diffusion flux in laminar flows, equation 2.325, is strictly valid when the mixture composition is not changing, or when  is independent of the composition. This is an acceptable approximation in dilute mixtures when
is independent of the composition. This is an acceptable approximation in dilute mixtures when  is very small for all the components except for the carrier gas. For nondilute mixtures in multicomponent laminar flows, you calculate
is very small for all the components except for the carrier gas. For nondilute mixtures in multicomponent laminar flows, you calculate 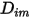 from the following formulation:
from the following formulation:
 is independent of the composition. This is an acceptable approximation in dilute mixtures when
is independent of the composition. This is an acceptable approximation in dilute mixtures when  is very small for all the components except for the carrier gas. For nondilute mixtures in multicomponent laminar flows, you calculate
is very small for all the components except for the carrier gas. For nondilute mixtures in multicomponent laminar flows, you calculate 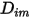 from the following formulation:
from the following formulation: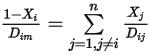
Equation 2.333
where 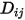 is the binary mass diffusion coefficient of component
is the binary mass diffusion coefficient of component  in component
in component  , which you need to specify or calculate.
, which you need to specify or calculate.
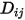 is the binary mass diffusion coefficient of component
is the binary mass diffusion coefficient of component  in component
in component  , which you need to specify or calculate.
, which you need to specify or calculate.◦ Specified Value—Binary mass diffusion coefficient 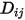 is a constant or function of temperature if heat transfer is accounted for. You can specify the value directly or obtain it from the specified Schmidt number:
is a constant or function of temperature if heat transfer is accounted for. You can specify the value directly or obtain it from the specified Schmidt number:
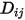 is a constant or function of temperature if heat transfer is accounted for. You can specify the value directly or obtain it from the specified Schmidt number:
is a constant or function of temperature if heat transfer is accounted for. You can specify the value directly or obtain it from the specified Schmidt number:
Equation 2.334
where,
 | Schmidt number |
Schmidt number is defined as the ratio of the viscous diffusion rate to the molecular (mass) diffusion rate.
If one value or one function of temperature applies for all the components, equation 2.333 is reduced to
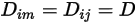
Equation 2.335
Equation 2.335 is an appropriate approximation for modeling a dilute mixture, with the species present at low mass fractions in a carrier fluid that has high concentration. In such cases, you define 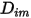 directly as a constant or a function of temperature.
directly as a constant or a function of temperature.
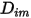 directly as a constant or a function of temperature.
directly as a constant or a function of temperature.However, for non-dilute mixtures, with the specified  , you use equation 2.333 to compute the individual mass diffusion coefficient in the mixture
, you use equation 2.333 to compute the individual mass diffusion coefficient in the mixture 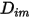 .
.
 , you use equation 2.333 to compute the individual mass diffusion coefficient in the mixture
, you use equation 2.333 to compute the individual mass diffusion coefficient in the mixture 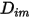 .
.◦ Kinetic Theory—For an ideal gas, the binary mass diffusion coefficient 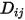 can also be obtained using kinetic theory.
can also be obtained using kinetic theory.
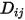 can also be obtained using kinetic theory.
can also be obtained using kinetic theory.References: H. A. McGee, “Molecular Engineering”, McGraw-Hill, New York, 1991.
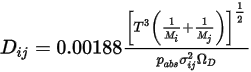
Equation 2.336
where 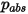 is the absolute pressure, and
is the absolute pressure, and 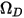 is the diffusion collision integral, which is a measure of the interaction of the molecules in the system.
is the diffusion collision integral, which is a measure of the interaction of the molecules in the system. 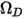 is a function of the quantity
is a function of the quantity 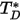 , defined as:
, defined as:
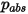 is the absolute pressure, and
is the absolute pressure, and 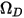 is the diffusion collision integral, which is a measure of the interaction of the molecules in the system.
is the diffusion collision integral, which is a measure of the interaction of the molecules in the system. 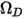 is a function of the quantity
is a function of the quantity 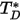 , defined as:
, defined as: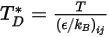
Equation 2.337
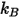 is the Boltzmann constant, which is defined as the universal gas constant
is the Boltzmann constant, which is defined as the universal gas constant 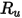 divided by the Avogadro number.
divided by the Avogadro number. 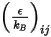 for the mixture is the geometric average:
for the mixture is the geometric average: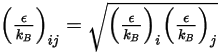
Equation 2.338
For a binary mixture, 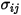 is calculated as the arithmetic average of the individual
is calculated as the arithmetic average of the individual 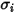 and
and 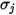 :
:
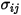 is calculated as the arithmetic average of the individual
is calculated as the arithmetic average of the individual 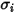 and
and 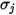 :
: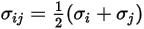
Equation 2.339
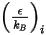 and
and 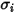 are the Lennard-Jones parameters for component
are the Lennard-Jones parameters for component  in the mixture. Specifically,
in the mixture. Specifically, 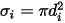 is the collision cross section of the sphere molecule with the diameter
is the collision cross section of the sphere molecule with the diameter 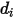 (note that a molecule sweeps out an area given by twice its diameter, as the molecules with which it collides also have diameter
(note that a molecule sweeps out an area given by twice its diameter, as the molecules with which it collides also have diameter 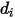 ); and
); and  =1.38064852(79) ×10-23(J/K) is the Boltzmann constant.
=1.38064852(79) ×10-23(J/K) is the Boltzmann constant.In Creo Flow Analysis, you specify the diameter  and the energy
and the energy 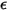 to determine the two Lennard-Jones parameters.
to determine the two Lennard-Jones parameters.
 and the energy
and the energy 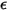 to determine the two Lennard-Jones parameters.
to determine the two Lennard-Jones parameters.◦ Thermal Diffusion Coefficients 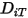 —Thermal Diffusion Coefficients can be defined as constants, polynomial functions of temperature, user-defined functions, or using the following empirically-based composition-dependent expression derived from:
—Thermal Diffusion Coefficients can be defined as constants, polynomial functions of temperature, user-defined functions, or using the following empirically-based composition-dependent expression derived from:
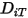 —Thermal Diffusion Coefficients can be defined as constants, polynomial functions of temperature, user-defined functions, or using the following empirically-based composition-dependent expression derived from:
—Thermal Diffusion Coefficients can be defined as constants, polynomial functions of temperature, user-defined functions, or using the following empirically-based composition-dependent expression derived from:References: K. K. Y. Kuo, “Principles of Combustion”, John Wiley and Sons, New York, 1986.
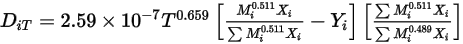
Equation 2.340
This form of the thermal diffusion coefficient causes heavy molecules to diffuse less rapidly, and light molecules to diffuse more rapidly, towards heated surfaces.
• Momentum Equations
With the mass-weighted properties and velocities, the momentum equations for the mixture of all the components have the same expression as those for single fluid flows:
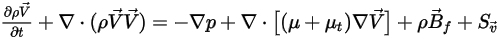
Equation 2.341
where the mixture density and velocity are calculated using equation 2.321, equation 2.322, and equation 2.323. The turbulent viscosity is directly computed from the turbulence models based on the mixture flow so that its value is independent of the components. For the laminar viscosity, it is computed as follows:
◦ Mass-Averaged Laminar Viscosity—For non-ideal gas mixtures, the mixture viscosity is calculated based on a mass fraction average of the pure chemical species (components) viscosities:
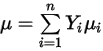
Equation 2.342
◦ Kinetic Theory—For ideal gas mixtures, the mixture viscosity is computed based on the kinetic theory. For each component, the dynamic viscosity is based on the Boltzmann equation:

Equation 2.343
For the mass diffusivity, you require the Lennard-Jones parameters, 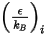 and
and 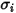 to calculate the viscosities of the gas components in a mixture.
to calculate the viscosities of the gas components in a mixture.
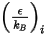 and
and 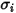 to calculate the viscosities of the gas components in a mixture.
to calculate the viscosities of the gas components in a mixture.Viscosity for the ideal gas mixture is then calculated as:
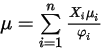
Equation 2.344
where,
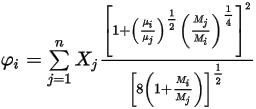
Equation 2.345
• Energy Equation
As described in the Heat module, the energy equation for the mixture of all the components is expressed as:

Equation 2.346
where 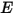 and
and 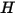 are the total internal energy and total enthalpy of the
are the total internal energy and total enthalpy of the 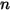 component mixture. Along with the mixture specific heat
component mixture. Along with the mixture specific heat  and static enthalpy
and static enthalpy 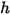 , they are obtained by mass-averaging the corresponding values of each component:
, they are obtained by mass-averaging the corresponding values of each component:
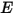 and
and 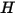 are the total internal energy and total enthalpy of the
are the total internal energy and total enthalpy of the 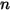 component mixture. Along with the mixture specific heat
component mixture. Along with the mixture specific heat  and static enthalpy
and static enthalpy 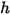 , they are obtained by mass-averaging the corresponding values of each component:
, they are obtained by mass-averaging the corresponding values of each component:◦ Mass-Averaged Mixture Heat Capacity
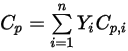
Equation 2.347
◦ Mass-Averaged Mixture Energy and Enthalpy
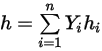
Equation 2.348
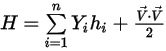
Equation 2.349
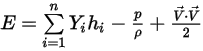
Equation 2.350
Static enthalpy of a component consists of two parts: standard state reference enthalpy and sensible enthalpy. For multicomponent flows, you include both parts of the enthalpy (the absolute or total value) when you calculate  .
.
 .
.In equation 2.336, the first term on the right side represents the diffusion of the energy. It consists of three parts: heat conduction, energy transport due to diffusion of the species, and viscous heating. For the mixture heat conduction, it is modeled in the same way as in the single fluid flow. In Creo Flow Analysis the mixture heat conductivity is calculated as follows:
◦ Mass-Averaged Heat Conductivity—For non-ideal gas mixtures, the mixture heat conductivity is computed based on a simple mass fraction average of the pure species or components heat conductivities:

Equation 2.351
This is the default method in Creo Flow Analysis.
◦ Kinetic Theory—For ideal gas mixtures, the mixture heat conductivity can be computed based on kinetic theory. For each component, the heat conductivity has the form:
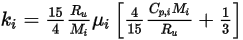
Equation 2.352
where,
 | universal gas constant |
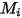 | molecular weight |
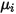 | specified or computed viscosity of the component |
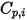 | specified or computed specific heat capacity of the component |
Note that as the laminar viscosity, 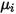 , the specific heat
, the specific heat 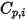 can also be obtained using kinetic theory:
can also be obtained using kinetic theory:
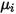 , the specific heat
, the specific heat 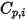 can also be obtained using kinetic theory:
can also be obtained using kinetic theory:
Equation 2.353
where 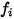 is the number of modes of energy storage (degrees of freedom) for the gas component
is the number of modes of energy storage (degrees of freedom) for the gas component  .
.
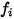 is the number of modes of energy storage (degrees of freedom) for the gas component
is the number of modes of energy storage (degrees of freedom) for the gas component  .
.The heat conductivity for the ideal gas mixture is then calculated as:
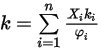
Equation 2.354
where  is expressed in equation 2.335.
is expressed in equation 2.335.
 is expressed in equation 2.335.
is expressed in equation 2.335.The second diffusion term,
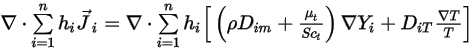
Equation 2.355
represents the transport of enthalpy due to the diffusion of the chemical species in the 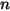 component flow. This term can have a significant effect on the enthalpy field and should not be neglected. When the Lewis number, the ratio of thermal diffusivity
component flow. This term can have a significant effect on the enthalpy field and should not be neglected. When the Lewis number, the ratio of thermal diffusivity  to mass diffusivity
to mass diffusivity 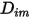 :
:
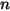 component flow. This term can have a significant effect on the enthalpy field and should not be neglected. When the Lewis number, the ratio of thermal diffusivity
component flow. This term can have a significant effect on the enthalpy field and should not be neglected. When the Lewis number, the ratio of thermal diffusivity  to mass diffusivity
to mass diffusivity 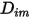 :
:
Equation 2.356
for any species is not unity, neglecting this term can result in significant errors.
The third diffusion term is the viscous heating contribution 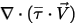 . Though it is treated in the same way as in the single fluid flow, you calculate the shear
. Though it is treated in the same way as in the single fluid flow, you calculate the shear 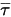 using the mixture laminar and turbulent viscosities. The general source term
using the mixture laminar and turbulent viscosities. The general source term 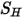 is the total external or user heat source on all the components.
is the total external or user heat source on all the components.
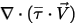 . Though it is treated in the same way as in the single fluid flow, you calculate the shear
. Though it is treated in the same way as in the single fluid flow, you calculate the shear 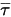 using the mixture laminar and turbulent viscosities. The general source term
using the mixture laminar and turbulent viscosities. The general source term 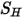 is the total external or user heat source on all the components.
is the total external or user heat source on all the components.• Turbulence Models—With the mixture density 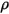 , molecular viscosity
, molecular viscosity 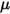 , and velocity
, and velocity 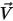 , the turbulence modeling equations in both the standard k-ε and RNG k-ε models have the same general forms as in the single fluid turbulence models. These are described in the Turbulence module. The turbulent viscosity for the mixture
, the turbulence modeling equations in both the standard k-ε and RNG k-ε models have the same general forms as in the single fluid turbulence models. These are described in the Turbulence module. The turbulent viscosity for the mixture  is computed directly from the expression:
is computed directly from the expression:
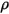 , molecular viscosity
, molecular viscosity 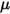 , and velocity
, and velocity 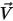 , the turbulence modeling equations in both the standard k-ε and RNG k-ε models have the same general forms as in the single fluid turbulence models. These are described in the Turbulence module. The turbulent viscosity for the mixture
, the turbulence modeling equations in both the standard k-ε and RNG k-ε models have the same general forms as in the single fluid turbulence models. These are described in the Turbulence module. The turbulent viscosity for the mixture  is computed directly from the expression:
is computed directly from the expression: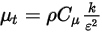
Equation 2.357
Also, the production of turbulent kinetic energy is calculated based on mixture turbulent viscosity and velocity gradients.
Modeling of Multicomponent Boundaries
In a multicomponent flow, boundary conditions for the flow, energy, and turbulence modeling equations are the same as those in the single phase flows, described in the Flow, Heat, and Turbulence modules. For the mass fractions of a component, the boundary conditions consist of specified value, specified volumetric flux, and/or gradient.
• n-Component Inlet Boundary
At an inlet boundary, the net transport of a component can consist of both convection and diffusion contributions. The convection is determined by the specified inlet species mass fraction. The diffusion depends on the gradient of the computed mass fraction field. At very small convective inlet velocities, substantial mass can be gained or lost through the inlet due to diffusion. For this reason, the inlet diffusion is not included by default, but can be enabled as an option.
◦ Specified Value—For 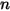 component flow, the inlet mass fractions are predetermined for
component flow, the inlet mass fractions are predetermined for 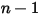 components, while the mass fraction of the
components, while the mass fraction of the  component is obtained using the physical constraint equation 2.319:
component is obtained using the physical constraint equation 2.319:
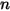 component flow, the inlet mass fractions are predetermined for
component flow, the inlet mass fractions are predetermined for 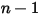 components, while the mass fraction of the
components, while the mass fraction of the  component is obtained using the physical constraint equation 2.319:
component is obtained using the physical constraint equation 2.319:
Equation 2.358
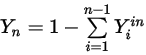
Equation 2.359
Also, the mass fraction for each component must be nonnegative.
◦ Specified Volumetric Flux—Assuming that 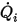 is the predescribed inlet volumetric flux for component
is the predescribed inlet volumetric flux for component  , you have the mass flux of each component
, you have the mass flux of each component 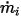 and the total mass flux at the inlet
and the total mass flux at the inlet 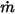 as:
as:
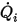 is the predescribed inlet volumetric flux for component
is the predescribed inlet volumetric flux for component  , you have the mass flux of each component
, you have the mass flux of each component 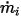 and the total mass flux at the inlet
and the total mass flux at the inlet 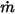 as:
as:
Equation 2.360
where 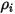 is the inlet density of the component
is the inlet density of the component  .
.
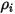 is the inlet density of the component
is the inlet density of the component  .
.By definition, the mass fraction is computed as:
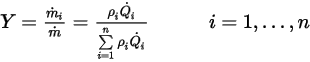
Equation 2.361
◦ Outlet, Symmetry, Wall Boundary—For  components, zero gradient conditions apply for all the outlet, symmetry, and wall boundaries, while the
components, zero gradient conditions apply for all the outlet, symmetry, and wall boundaries, while the 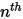 phase is obtained using the physical constraint:
phase is obtained using the physical constraint:
 components, zero gradient conditions apply for all the outlet, symmetry, and wall boundaries, while the
components, zero gradient conditions apply for all the outlet, symmetry, and wall boundaries, while the 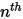 phase is obtained using the physical constraint:
phase is obtained using the physical constraint: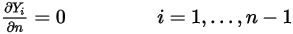
Equation 2.362

Equation 2.363
where  is the boundary value obtained from equation 2.347.
is the boundary value obtained from equation 2.347.
 is the boundary value obtained from equation 2.347.
is the boundary value obtained from equation 2.347.Numerical Considerations
The above governing equations, turbulence models, and boundary conditions form the foundation of the multicomponent mixing model. Without external or user source terms and chemical reactions, they are a closed system of equations that you solve numerically using a pressure-based finite volume solver.
The mass-fraction transport equations are solved for all the components. To satisfy the physical constraint, the actual mass fractions are scaled by the sum of the solved values for all the components:

Equation 2.364
where 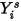 is the value obtained from solving equation 2.320. The actual mass fraction is:
is the value obtained from solving equation 2.320. The actual mass fraction is:
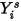 is the value obtained from solving equation 2.320. The actual mass fraction is:
is the value obtained from solving equation 2.320. The actual mass fraction is: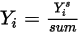
Equation 2.365