Modelado de erosión por partículas
La erosión es un fenómeno que provoca la pérdida de material debido al impacto repetido de partículas sólidas en una superficie. La erosión daña los tubos, las válvulas y otros pasos de flujo. Por lo tanto, es importante estudiar la velocidad de erosión e identificar las áreas susceptibles de erosión en los pasos de flujo.
En el modelado de erosión basado en CFA se incluyen los siguientes pasos:
1. Los datos de campo de flujo, tales como la velocidad, se obtienen al resolver las ecuaciones de Navier-Stokes.
2. Las partículas se liberan en el campo de flujo y se realiza un seguimiento individual para obtener información como, por ejemplo, la velocidad de impacto y el ángulo de impacto.
3. La información de impacto de las partículas se utiliza en una ecuación de erosión para calcular la tasa/velocidad de erosión o la pérdida de masa de la superficie causada por el impacto de las partículas.
Las ecuaciones de erosión estudian los efectos de los distintos parámetros en la erosión, tales como:
Referencias: Mazdak Parsi et al. "A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications" (2014)
• Características de las partículas, tales como el tamaño, la forma, la densidad, la dureza, etc.
• Información sobre el impacto de las partículas, como la velocidad de impacto de la partícula 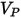 , el ángulo de impacto
, el ángulo de impacto 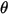 , la interacción partícula-partícula, etc.
, la interacción partícula-partícula, etc.
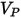 , el ángulo de impacto
, el ángulo de impacto 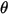 , la interacción partícula-partícula, etc.
, la interacción partícula-partícula, etc.• Propiedades de la pared de destino, como la densidad del material, la dureza, etc.
Las ecuaciones de erosión calculan la tasa de erosión 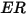 , definida como la cantidad de pérdida de material de pared (debido al impacto de partículas sólidas) dividida por la masa de las partículas sólidas que impactan.
, definida como la cantidad de pérdida de material de pared (debido al impacto de partículas sólidas) dividida por la masa de las partículas sólidas que impactan.
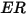 , definida como la cantidad de pérdida de material de pared (debido al impacto de partículas sólidas) dividida por la masa de las partículas sólidas que impactan.
, definida como la cantidad de pérdida de material de pared (debido al impacto de partículas sólidas) dividida por la masa de las partículas sólidas que impactan.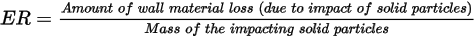
Creo Flow Analysis utiliza los modelos de erosión detalladas en las siguientes secciones:
Referencias: Mazdak Parsi etc. "CFD simulation of sand particle erosion in gas-dominant multiphase flow" (2015)
Modelo de Finne
La ecuación de erosión de Finne es la siguiente:
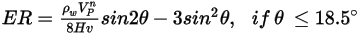
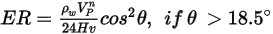
donde,
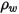 | densidad del material de pared (kg/m3) |
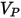 | velocidad de impacto de la partícula (m/s) |
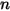 | exponente de velocidad (igual a 2 para la mayoría de las aplicaciones industriales) |
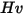 | Dureza Vicker (Pa) |
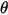 | ángulo de impacto (grados) |
En este modelo se subestima la eliminación de material para los ángulos de impacto de partícula mayores que 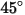 y no se prevé ninguna erosión para impactos normales. y no se prevé ninguna erosión para impactos normales. |
Modelo de Zhang
La ecuación de erosión de Zhang es la siguiente:
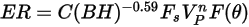
donde,
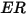 | tasa de erosión |
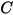 | 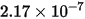 |
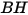 | Dureza Brinell del material de pared (Pa) |
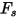 | factor de forma de partícula |
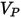 | velocidad de impacto de la partícula (m/s) |
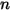 | exponente de velocidad (igual a 2.41) |
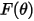 | función de ángulo de impacto |
El factor de forma de partícula 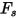 tiene los siguientes valores para distintos tipos de partículas de arena:
tiene los siguientes valores para distintos tipos de partículas de arena:
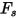 tiene los siguientes valores para distintos tipos de partículas de arena:
tiene los siguientes valores para distintos tipos de partículas de arena:Valor | Tipo de partícula de arena |
|---|---|
1.0 | viva o angular |
0.53 | semiredondeada |
0.2 | completamente redondeada |
La función de ángulo de impacto se proporciona de la siguiente manera:
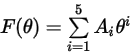
En la siguiente tabla se indican los valores de 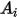 :
:
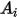 :
: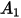 | 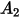 | 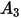 | 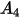 | 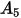 |
|---|---|---|---|---|
5.40 | -10.11 | 10.93 | -6.33 | 1.42 |
Modelo de Oka
La ecuación de erosión de Oka et al. es la siguiente:
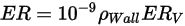
Ecuación 2.406
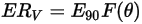
Ecuación 2.407
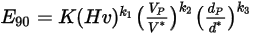
Ecuación 2.408
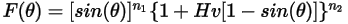
Ecuación 2.409
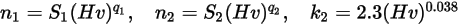
Ecuación 2.410
donde,
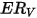 | tasa de erosión volumétrica (mm3/kg) |
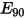 | daños por erosión con un ángulo de impacto normal (mm3/kg) |
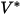 | velocidad de impacto de referencia (m/s) |
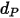 | diámetro de partícula (m) |
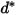 | diámetro de partícula de referencia (m) |
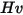 | Dureza Vicker (GPa) |
Los valores de los diferentes coeficientes que se utilizan en la ecuación 2.406, la ecuación 2.407, la ecuación 2.408, la ecuación 2.409 y la ecuación 2.410 aparecen en la siguiente tabla:
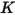 | 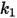 | 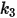 | 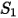 | 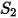 | 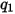 | 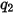 |
|---|---|---|---|---|---|---|
60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
Modelo de DNV
La ecuación de erosión de DNV es la siguiente:
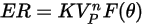
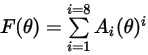
donde,
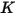 | 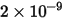 |
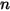 (exponente de velocidad) (exponente de velocidad) | 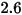 |
En la siguiente tabla se indican los valores de 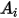 :
:
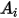 :
: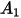 | 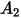 | 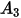 | 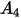 | 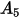 | 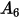 | 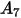 | 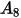 |
|---|---|---|---|---|---|---|---|
9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Modelo de Mansouri
Mansouri desarrolló una ecuación de erosión, tal como se indica a continuación:
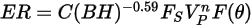
Ecuación 2.413
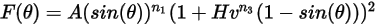
Ecuación 2.414
donde,
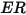 | tasa de erosión |
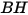 | Dureza Brinell del material de pared (Pa) |
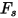 | factor de forma de partícula |
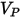 | velocidad de impacto de la partícula (m/s) |
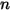 | exponente de velocidad |
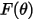 | función de ángulo de impacto |
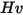 | Dureza Vicker (Pa) |
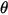 | Ángulo de impacto (grados) |
En la siguiente tabla se incluyen los valores de diferentes parámetros que se utilizan en la ecuación 2.413 y la ecuación 2.414 de la ecuación de erosión de Mansouri (2015).
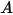 | 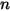 | 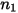 | 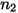 | 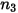 | 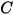 |
|---|---|---|---|---|---|
0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49e-07 |
Modelo de Grant-Tabakoff
La ecuación de erosión del modelo de Grant-Tabakoff es la siguiente:
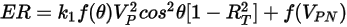
Ecuación 2.415
donde,
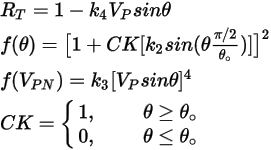
Ecuación 2.416
donde,
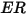 | tasa de erosión |
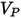 | velocidad de impacto de la partícula (m/s) |
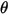 | ángulo de impacto (grados) |
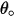 | ángulo de la erosión máxima (grados) |
La tasa de erosión 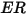 en la ecuación 2.415 se define como la cantidad, en miligramos, de material eliminado por unidad de masa (g) de las partículas impactantes. La unidad de velocidad es pie/s.
en la ecuación 2.415 se define como la cantidad, en miligramos, de material eliminado por unidad de masa (g) de las partículas impactantes. La unidad de velocidad es pie/s.
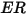 en la ecuación 2.415 se define como la cantidad, en miligramos, de material eliminado por unidad de masa (g) de las partículas impactantes. La unidad de velocidad es pie/s.
en la ecuación 2.415 se define como la cantidad, en miligramos, de material eliminado por unidad de masa (g) de las partículas impactantes. La unidad de velocidad es pie/s.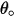 es el ángulo de la erosión máxima. Por ejemplo,
es el ángulo de la erosión máxima. Por ejemplo, 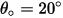 para la aleación basada en aluminio.
para la aleación basada en aluminio.Los valores de los diferentes coeficientes para el modelo de Grant-Tabakoff se encuentran en la siguiente tabla:
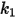 | 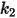 | 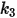 | 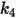 |
3.67e-06 | 0.585 | 6e-12 | 0.0016 |