Transferencia de calor
Flujo laminar a través de una tubería con flujo térmico uniforme
Exposición del problema: el flujo laminar 3D con transferencia de calor se modela en una tubería mediante el módulo de calor. El fluido entra en la tubería a 300 K y se calienta mediante un flujo térmico uniforme en la pared de la tubería.

à: perfil de velocidad completamente desarrollado a 300 K
Referencias: F.M. White. Fluid Mechanics. 3rd Edition. McGraw Hill Book Co. Inc., New York, NY, 1994.
Propiedades de fluido | Propiedades geométricas | Condiciones de trabajo |
|---|---|---|
Densidad = 13529 kg/m3 Viscosidad = 0.001523 Pa-s Calor específico = 139.3 J/kg-K Conductividad = 8.54 W/m-K | R = 0.0025 m L = 0.1 m | Entrada = perfil de velocidad completamente desarrollado a 300 K Salida = 101325 Pa Փq = 5000 W/m2 |
Comparación de resultados: pérdida de presión y temperatura de salida
Resultados | Solución analítica | Creo Flow Analysis | Error porcentual |
|---|---|---|---|
Caída de presión (Pa) | 1 | 1.0054 | 0.54 |
Temperatura de salida (K) | 340 | 340.894 | 0.26 |
Convección natural en un anillo concéntrico
Exposición del problema: la convección natural se modela en un anillo concéntrico mediante el módulo de calor. La pared interna del anillo concéntrico está 50 K más caliente que la pared exterior.

A = plano de simetría
Referencias: T.H. Kuehn, R.J. Goldstein, "An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli", Journal of Heat Transfer, Vol 100, pp. 635-640, 1978.
Propiedades de fluido | Propiedades geométricas | Condiciones de trabajo |
|---|---|---|
Densidad = gas o aire ideal Viscosidad = 3.54822 x 10-5 Pa-s | Perfil aerodinámico RAE 2822 AoA = 2.31 grados Altura del túnel de viento = 72 m Longitud de túnel de viento = 96 m | R1 = 0.0178 m T1 = 373 R2 = 0.04628 m T2 = 327 |
Resultado: contornos de temperatura
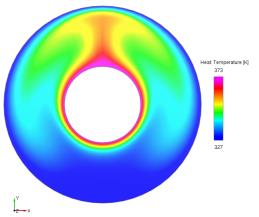
Comparación de resultados: distribución de temperatura a lo largo de la pared simétrica

Comparación de resultados: comparación con datos de imagen térmica

Conducción en un bloque sólido compuesto
Exposición del problema: la conducción se modela en un bloque sólido compuesto formado por dos materiales mediante el módulo de calor. Un flujo térmico definido en la pared derecha del bloque calienta el sistema.
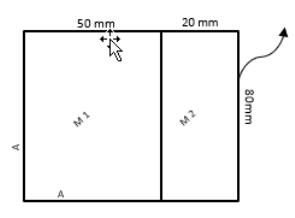
• A = pared adiabática
• M 1 = material 1
◦ Densidad = 2719 kg/m3
◦ Calor específico = 871 J/kg-K
◦ Conductividad térmica = 75 W/m-K
◦ Calor generado = 1.5 * 106W/m3
• M 2 = material 2
◦ Densidad = 8978 kg/m3
◦ Calor específico = 381 J/kg-K
◦ Conductividad térmica = 150 W/m-K
Referencias: F.P. Incropera, D.P. Dewitt.Fundamentals of Heat and Mass Transfer. 5ª edición, pág. 117, 2006.

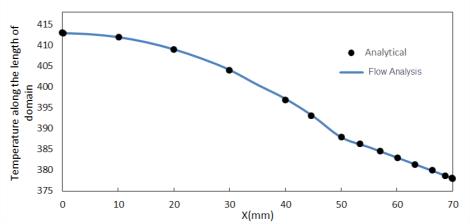
Comparación de resultados: temperatura en todo el bloque compuesto
Conducción transitoria en un lingote semiinfinito
Exposición del problema: un lingote semiinfinito se calienta durante 120 segundos mediante un flujo térmico uniforme definido en la pared izquierda del lingote. El lingote se mide y las medidas se comparan con la solución analítica.

• S = simetría
• A = pared adiabática
Referencias: F.P. Incropera, D.P. Dewitt, T.L. Bergman, A.S. Lavine, Introduction to Heat Transfer, 5th edition, Wiley and sons, 2007.
Propiedades de sólido | Propiedades geométricas | Condiciones de trabajo |
|---|---|---|
Densidad = 8995.64 kg/m3 Calor específico = 381 J/kg-K Conductividad = 401 W/m-K | L = 0.75 m H = 0.1 m | Transitorio = 120 s Փq = 3 x 105 W/m2 Temperatura inicial = 293 K |
Resultado: contornos de temperatura

Comparación de resultados: la temperatura sube en todo el lingote.
