亂流模型
您可以根據渦流黏度模型來計算流體系統中的有效亂流黏度。渦流黏度模型中有兩個模型:
• 標準 K-Epsilon 模型
標準 K-Epsilon 模型是 Creo Flow Analysis 中可用的一種「亂流」(Turbulence) 模型。
亂流動能 k 的公式如下:
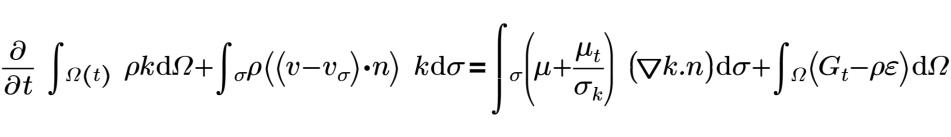
亂流消散率 ε 的公式如下:
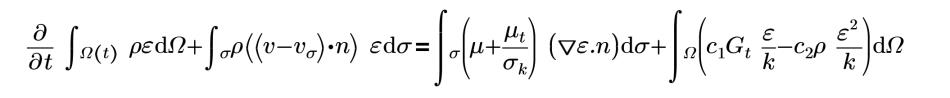
其中,
c1=1.44 | 常數 C1 |
c2=1.92 | 常數 C2 |
σk=1 | 亂流動能普朗特數 |
σz=1 | 亂流消散率普朗特數 |
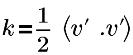 | 亂流動能 |
v' | 亂流波動速度 |
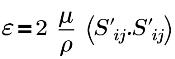 | 亂流動能消散率 |
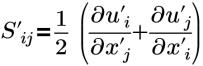 | 應變張量 |
u'i(i=1,2,3) | 亂流波動速度的分量 |
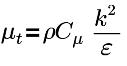 | 亂流黏度,且 Cμ=0.09,E=9.793 |
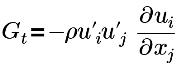 | 亂流產生期 |
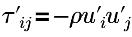 | 亂流雷諾應力 |
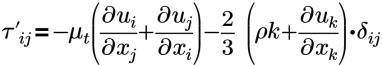 | 雷諾應力的布新尼斯 (Boussinesq) 近似 |
參考:Launder, B.E. & Spalding, D.B. (1974) “The numerical computation of turbulent flows,” Computer Methods, Applied Mechanics and Engineering, vol. 3 冊,頁269-289
• 重整化群組 (RNG) K-Epsilon 模型
重整化群組 (RNG) K-Epsilon 模型是 Creo Flow Analysis 中可用的一種「亂流」(Turbulence) 模型。此模型類似於標準 K Epilson 模型,但其運算式包含兩個新常數,用於修正以下方程式中的 C2 RNG 項:
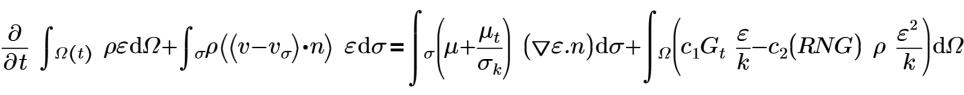
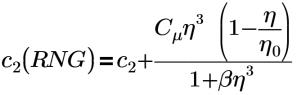
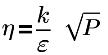
其中,
η0=4.38 | RNG 常數 (Flow Analysis 中的寫死常數) |
β=1.92 | RNG 常數 (Flow Analysis 中的寫死常數) |
P | 局部壓力 |
c1=1.44 | 常數 C1 |
c2=1.92 | 常數 C2 |
σk=1 | 亂流動能普朗特數 |
σz=1 | 亂流消散率普朗特數 |
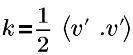 | 亂流動能 |
v' | 亂流波動速度 |
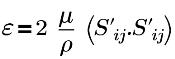 | 亂流動能消散率 |
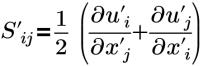 | 應變張量 |
u'i(i=1,2,3) | 亂流波動速度的分量 |
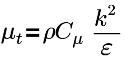 | 亂流黏度,且 Cμ=0.09 |
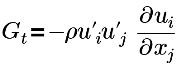 | 亂流產生期 |
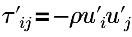 | 亂流雷諾應力 |
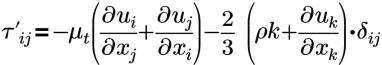 | 雷諾應力的布新尼斯 (Boussinesq) 近似 |
參考:Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, pp1510-1520