定义
• 自然频率 - 一秒内发生的运动周期数。通过弹簧常数 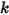 和质量
和质量 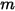 计算得出。
计算得出。
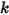 和质量
和质量 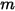 计算得出。
计算得出。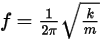
其中,
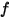 | 自然频率 (Hz) |
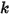 | 弹簧常数 |
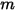 | 质量 (kg) |
• 零位移 - 模型构建期间动力学边界所在的位置。其中可包含相对于构建位置的偏移量,这样,如果位移为零,动力学边界即不会与构建位置相对应。
• 位移 (m) - 平移 (1 DOF) ODE 中动力学边界相对于其零位移位置发生线性平移的大小。对于规定的运动条件,位移等于规定位移。
• 速度 (m/s) - 平移 (1 DOF) ODE 中动力学边界的速度的大小。如速度为正,表示其方向与移动方向相同。对于规定的运动,速度等于规定位移对时间的导数。
• 加速度 (m/s2) - 动力学边界的加速度的大小。对于规定的运动,加速度等于规定位移内速度对时间的导数。
• 阻尼力 (N) - 用于控制振动体的运动的力。例如,在弹簧中,空气可充当阻尼介质。如阻尼力为正,表示其方向与移动方向相同。
• 弹簧常数 - 力平衡方程中弹簧力所涉变量。与弹簧常数关联的弹簧力会抵抗位移的增加。
• 弹簧力 (N) - 由预紧力、弹簧常数和位移来确定。如弹簧力为正,表示其方向与移动方向相同。
• 弹簧预紧力 (N) - 当位移为零位移时弹簧所产生的力。零位移与初始位移不同。与此力关联的弹簧力会抵抗位移的增加。
• 流体力 (N) - 液动力包括压力和剪切力。如流体力为正,表示其方向与移动方向相同。
• 摩擦力 (N) - 由接触力的法向分量和摩擦系数来确定。
• 净力 (N) - 各力项 (例如液动力、阻尼力、由弹簧预紧力与弹簧常数 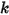 所确定的弹簧力、接触摩擦力以及施加于主体的任何附加力) 的共同作用效果。如净力为正,表示其方向与移动方向相同。
所确定的弹簧力、接触摩擦力以及施加于主体的任何附加力) 的共同作用效果。如净力为正,表示其方向与移动方向相同。
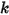 所确定的弹簧力、接触摩擦力以及施加于主体的任何附加力) 的共同作用效果。如净力为正,表示其方向与移动方向相同。
所确定的弹簧力、接触摩擦力以及施加于主体的任何附加力) 的共同作用效果。如净力为正,表示其方向与移动方向相同。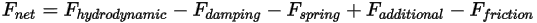
其中,
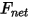 | 净力 (N) |
 | 液动力 (N) |
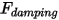 | 阻尼力 (N) |
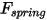 | 弹簧力 (N) |
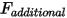 | 附加力 (N) |
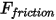 | 剪切力 (N) |
• 零角位移 - 在模型构建期间动力学边界所在的位置。其中可包含相对于构建位置的偏移量,这样,如果角位移为零,动力学边界即不会与构建位置相对应。
• 角位移 (度) - 动力学边界相对于其零角位移位置旋转的幅值。角度和正旋转方向由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示角度以逆时针方向为正。对于规定的运动,角位移等于规定的角位移。
• 角速度 (rad/s) - 动力学边界的角速度的大小。角速度的正负号由右手定则和旋转 (1 DOF) 模块的旋转轴矢量来确定,这样一来,如果旋转轴指向观察者,即表示角速度以逆时针方向为正。对于规定的运动,角速度等于规定角度对时间的导数,其单位为 rad/s。
• 角加速度 (rad/s2) - 旋转 (1 DOF) ODE 中动力学边界相对于零角位移位置旋转的幅值。角度和正加速度方向由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示角度以逆时针方向为正。对于规定的运动,角加速度等于规定角位移内角速度随时间的变化率。
• 阻尼扭矩 (N-m) - 由角速度和阻尼系数来确定。阻尼扭矩的正负号由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示阻尼扭矩以逆时针方向为正。
• 流体扭矩 (N-m) - 液动扭矩。流体扭矩的正负号由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示流体扭矩以逆时针方向为正。
• 弹簧扭矩 (N-m) - 由位移角、扭转预紧扭矩和扭转常数来确定。弹簧扭矩的正负号由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示弹簧扭矩以逆时针方向为正。
• 制动扭矩 (N-m) - 由于阻尼作用而产生的制动扭矩。其由旋转速度 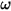 和用户定义的阻尼系数来确定。
和用户定义的阻尼系数来确定。
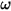 和用户定义的阻尼系数来确定。
和用户定义的阻尼系数来确定。• 净扭矩 (N-m) - 各扭矩项 (例如液动扭矩、阻尼力、由于扭转预紧扭矩和扭转常数所确定的弹簧扭矩,以及任何附加扭矩和接触摩擦力) 的共同作用效果。净扭矩的正负号由旋转轴矢量和右手定则来确定,这样一来,如果旋转轴指向观察者,即表示净扭矩以逆时针方向为正。
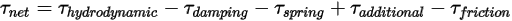
其中,
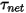 | 净扭矩 (N-m) |
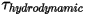 | 液动扭矩 (N-m) |
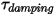 | 阻尼扭矩 (N-m) |
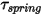 | 弹簧扭矩 (N-m) |
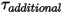 | 附加扭矩 (N-m) |
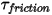 | 剪切扭矩 (N-m) |