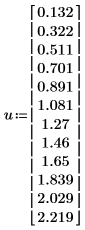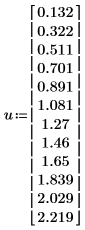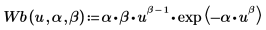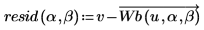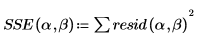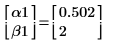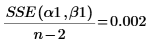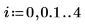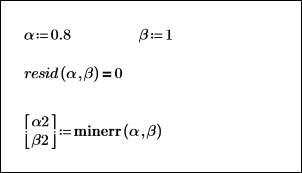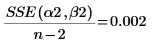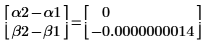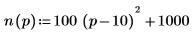任務 2 - 3:非線性最小平方擬合
擬合可建立數據組模型的函數參數。使用解題指令群最小化數據組與擬合函數之間的殘差。至於其他最佳化問題,您也可以重新排列問題以求解根。在此,將殘差設為零。
1. 定義數據集。
2. 定義擬合函數 Weibull 以及不明的參數 α 與 β。
3. 定義殘差,即數據組的 v 值與 v 值 (以 Wb 計算) 之間的差分。
4. 定義平方和。
5. 若要求解最佳擬合 Weibull 函數的參數 α 與 β,請插入解題指令群、定義 α 與 β 的估值,然後呼叫 minimize 函數。
6. 計算解。
7. 計算均方誤差。存在正解時,此值為零。
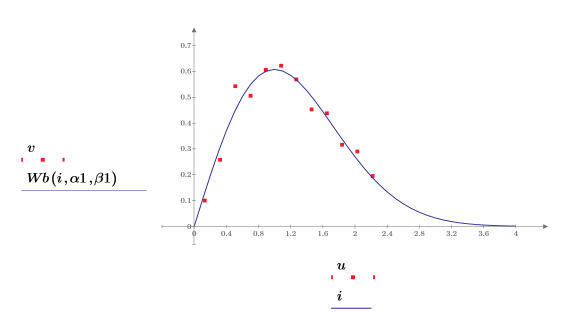
8. 繪製數據集與擬合的 Weibull 函數。
9. 若要使用條件約束 resid = 0 擬合參數,請使用 minerr 函數取代 minimize 函數。
此處無法使用 find 函數,因為沒有 α2 及 β2 的精確解。傳回錯誤,表示沒有任何解。minerr 函數的運作方式與 find 函數相同,唯一的差別是其若無法收斂成解 (落於一組疊代數內),即會傳回近似解。
10. 計算新參數的均方誤差。
11. 比較 minimize 及 minerr 傳回的結果。
練習
開始下個練習之前,請先求出假設希望獲得最大收益 n ∙ p 時的品項價格。函數 n 會說明售出品項數量與價格之間的關係:
先繪製 0 < p < 10 的利潤函數,再選擇估值。