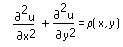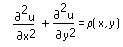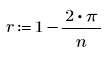PDE 的鬆弛法
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
傳回方形矩陣,其中矩陣內的元素位置會對應至其在方形區域中的位置,而且元素值會逼近普松偏微分方程式 (PDE)
在該點的解。relax 函數可使用修改過之 Gauss-Seidel 以及逐次超鬆弛法,求解普松方程式。
multigrid 函數可使用 multigrid 方法求解 U 的邊界條件全部為 0 時的特殊情況。
• 若邊界條件為常數且四邊都相等,請將方程式的邊界條件轉換成各邊都為 0,並使用 multigrid,因為這樣的速度較快且易於設定。
• 當 ρ = 0 時,普松方程式會降為拉普拉斯方程式。
• 若嘗試求解雙曲線或拋物線 PDE 或 PDE 系統,請使用 numol。
引數
• A, B, C, D, E 是相同大小的實數方形矩陣,內含函數 u 在四個最近鄰點及近似點之離散拉普拉斯近似係數。
• S 是內含位於方形內各點之來源項的方形矩陣。
• U 是方形矩陣,內含區域沿邊的邊界值以及在區域內解答的初始估值。
• rjac 是實數值 0 < rjac < 1,雅可比迭代法的頻譜半徑。此可控制鬆弛演算法的收斂。
rjac 最理想的值取決於問題的明細而定,但 r 是不錯的起始值,其中,n 是格點上各個方向的點數:
• M 是 1 + 2n 的方形矩陣,其元素對應到方形域中對應點的來源項。
• ncycle 是各層級 multigrid 疊代的循環整數。
ncycle 值 2 一般可提供適當的近似解。