函數 > 三角、對數與指數 > 指數與對數函數
  
指數與對數函數
• exp(z) - 傳回數字 e 的 z 次方。
• log(z, [b]) - 傳回 z 的基底 b 對數。若省略 b，則傳回 z 基底 10 的對數。
• ln(z) - 傳回 z 的自然對數 (基底 e)。
• ln0(z) - 傳回 z 的自然對數 (基底 e)，但在 z = 0 時會傳回 –1×10307。
引數
• z 必須是不具維度的純量 (實數、複數或虛數)，或為純量向量。
就函數 log 與 ln 而言，z 不可為零。若 z 為向量，則其所有的元素都不可為零。
• b (選用) 是正數的實數純量或純量向量。若省略，則 b 假定為 10。
若 b 為向量，則其所有的元素都不可為零，且其長度必須與向量 z 相同。
* 
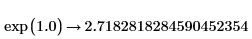• 若是複數 z，log 函數會傳回這些函數的主分支值，或 ln(z) = ln(|z|) + i arg(z)
• exp 函數相當於指定 e 為次方，但這兩者皆使用與標準指數不相同的演算法。針對指數的極大或極小值，此演算法可避免數值捨入誤差，較為健全。針對大量引數，使用 exp(x) 搭配小數引數進行符號計算，可求解最精確的值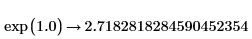：