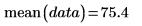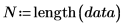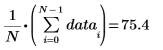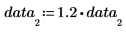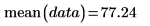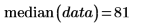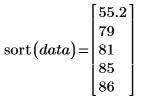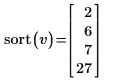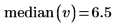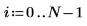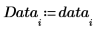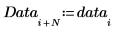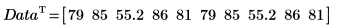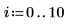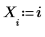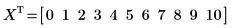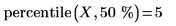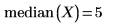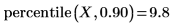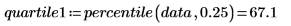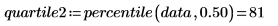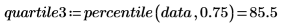範例:定位預期法
使用 mean、median、mode 及 percentile 函數提供與其餘分佈相關之數據點的位置量測。定位預期法的最佳選擇,視數據的一般離散或分佈而定。
mean
求解數據集的算術平均值。
1. 定義一組數值數據。
2. 使用 mean 函數計算數據的算術均數。
此相當於下列計算:
3. 重新計算均數之前,請先變更其中一個數據點。
均數對於在一或多個數據點之值的變更相當敏感。若數據集有顯著的離群值,會發現平均值無法適切地描述中央位置。您可裁剪離群值,並計算裁剪後的均數以獲得較佳的估值。
median
求解數據集的中值或中間值。
1. 使用 median 函數求解上一個數據集的中值。
2. 使用 sort 函數以升序對數據進行排序,並顯示中值是集合的中間值︰
中值取決於數據的相對位置,不會位於每一個數據點的實際值上。因此,相對於個別數據值中的小變化,中值即顯得較不敏感。
3. 使用 median 函數求解數據點中某個偶數的中值。
當數據集包含偶數的數據點時,中值是兩個中間數據點的平均值。
mode
數據集的模式是最大頻率時出現的值。
1. 使用 mode 函數求解數據集的模式。由於數據中沒有重複的值時,因此傳回錯誤。
2. 建立新數據集,其中包含一個以上重複相同頻率的元素。
3. 使用 mode 函數,以顯示多個數據值以相同的頻率重複時所傳回的錯誤。
percentile
使用 percentile 函數求解數據集的百分位數、四分位數及中值。百分位數會量測數據集中低於總點數特定百分比的值。
1. 定義數據集。
2. 使用 percentile 函數求解數據集 X 的第 50 個百分位數。
此等同於數據集 X 的中值:
3. 使用 percentile 函數求解數據集 X 的第 90 個百分位數。
第 90 個百分位數會出現在兩個數據點之間。
4. 使用 percentile 函數求解第一個數據集的四分位數。
四分位數是標記數據的 1/4 之三個百分位數之一。四分位數可用於分位數圖之數據圖的圖表分析。