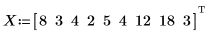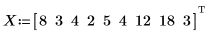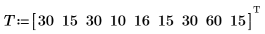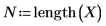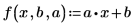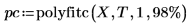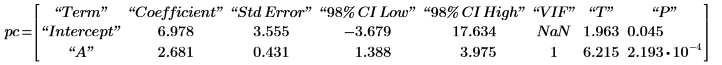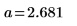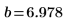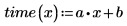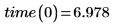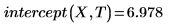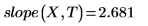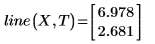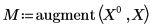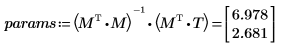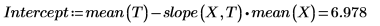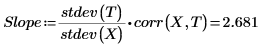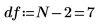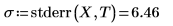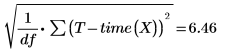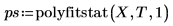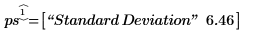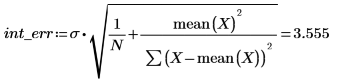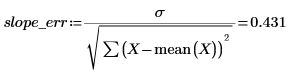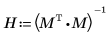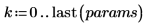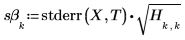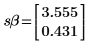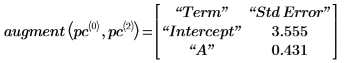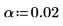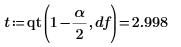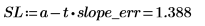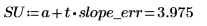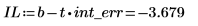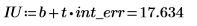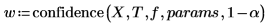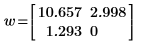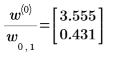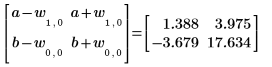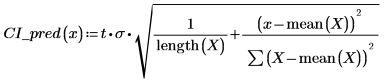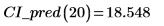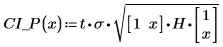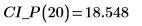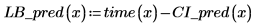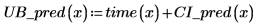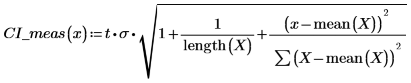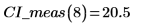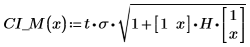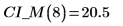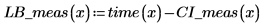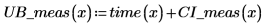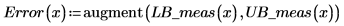範例:線性遞歸
使用 polyfitc、line、slope 及 intercept 函數,利用 x-y 數據集求解最佳擬合的最小平方線。使用 stderr 函數計算擬合參數的誤差。計算最佳擬合線附近的信心限制,並形成信心區間。
最佳擬合線
建立線性函數,預測行駛不同距離所需要的時間。
1. 定義以英哩計的距離集合,以及行駛這些距離所需要的分鐘數。
2. 定義單變量線性遞歸方程式。
3. 呼叫 polyfitc 計算遞歸 a 與 b 的係數。
係數如同 T 中各值的差異,而遞歸方程式 f 計算的值則是各 x 值的最小值。使用解題指令群與 minimize 函數最小化平方和,即可檢查此項:
4. 定義最佳擬合線,其會最小化各點到線之距離的平方和。
線性或任何其他類型遞歸的參數化方程式,應只用在接近原始觀測數據的值上。上述數據的最佳擬合線,預測旅行 0 英哩需要下列時間:
量測時間若僅是固定速度的旅行時間,則完全沒有意義。此類結果有時可代表特定的物理現象。在本例中,行駛零英哩所需的時間,可能會解釋成遇上交通號誌的平均等候時間。
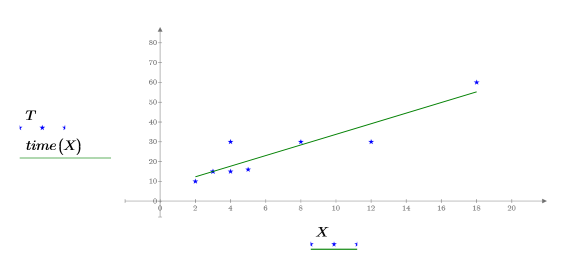
5. 繪製數據點與最佳擬合線。
計算斜率與截距的替代方法
有數種方法可計算最佳擬合線的斜率與截距。例如,line 函數會結合 slope 及 intercept 函數。包含矩陣計算或統計關係在內的其他方法。
1. 呼叫 intercept 與 slope 函數。
2. 呼叫 line 函數。
3. 利用 augment 函數來使用矩陣計算。
4. 利用 stdev、corr、mean 及 slope 函數來使用統計關係。
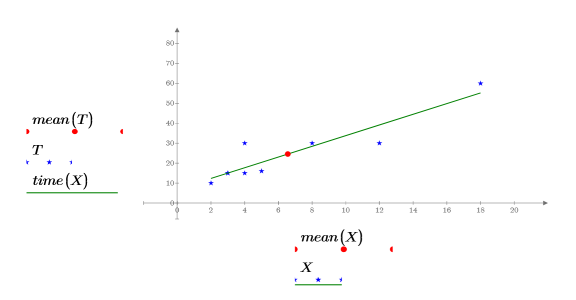
5. 使用繪圖顯示最小平方線一律會通過 (mean(X), mean(T)) 點:
標準誤差
計算預測的標準誤差 (亦稱之為標準誤差),以量測上述線性擬合的良適程度。也會計算斜率與截距的誤差。
1. 定義自由度 (數據點數減去擬合參數的數目)。
2. 呼叫 stderr 函數計算前文所定義之最佳擬合線的預測標準誤差。
此為均方誤差的平方根 MSE,或 σ2:
3. 使用 polyfitstat 函數傳回的標準誤差,與計算過的標準誤差進行比較。
4. 計算斜率與截距的標準誤差。
5. 使用矩陣計算重複上述計算。
6. 使用 augment 函數顯示每個遞歸係數的標準誤差,都記錄在 polyfitc 函數傳回的矩陣中。
每項係數的信心區間
使用前文的估值,加上 T-測試百分位數點,一併建立斜率與截距的估算信心區間。
1. 定義 98% 信心區間的顯著程度,並使用函數 qt 計算 t 係數。
2. 計算斜率的信心限制。
實際的斜率值有 98% 的機會落在 SL 與 SU 之間。
3. 計算截距的信心限制。
此值的廣大範圍反映數據中的高度散佈。
4. 呼叫 confidence 函數重複步驟 1 至 3。
confidence 函數傳回其第一欄的信心區間寬度,以及第二欄的 t 係數。當寬度除以 t 係數時,兩個參數都會得到標準誤差:
5. 若要求解信心限制,請加上或減去相關參數的寬度:
6. 使用 augment 函數顯示每個遞歸係數的標準誤差,都記錄在 polyfitc 函數傳回的矩陣中。
遞歸的信心區間
1. 使用函數 length 與 mean 計算遞歸本身的信心區間。
2. 使用上述函數計算任何預測 x 值的信心區間:
3. 使用矩陣計算:
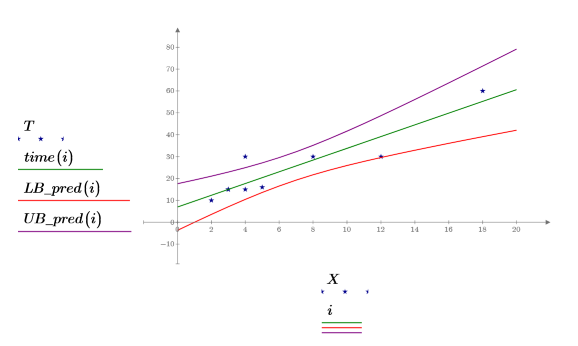
4. 繪製整個遞歸區域的數據、最佳擬合線及信心區間。
預測值的信心區域在靠近量測值中心的位置呈現腰狀。這是因為計算遞歸所用的公式,以均數為基礎,所以比較接近數據均數的預測值較準確。
5. 計算量測值上的信心限制。這些限制與預測值限制略有不同。
6. 使用矩陣計算:
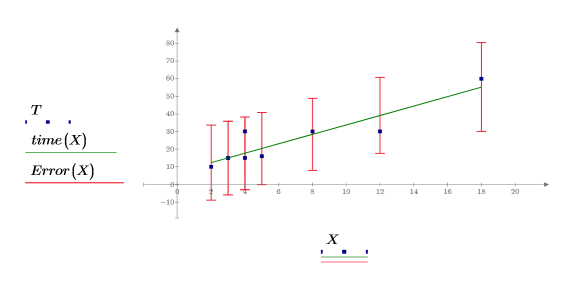
7. 將信心限制繪製為誤差繪線。
| 您可使用這些圖表作為離群值檢測的方式,落在信心區間之外的量測值即表示離群值。 |