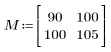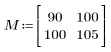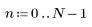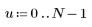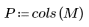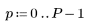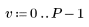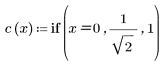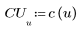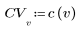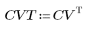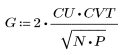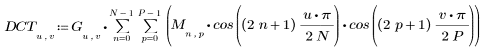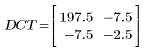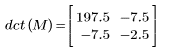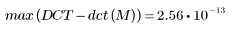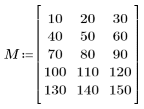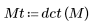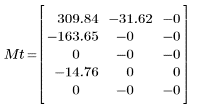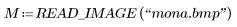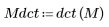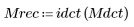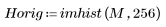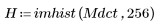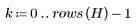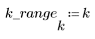範例:離散餘弦轉換
使用 dct 與 idct 函數分別計算離散餘弦轉換與逆轉換。此轉換在一些頻率元件中,具有集中在大部份圖像之「能量」或資訊的優點,因此適用於編碼。
如需使用此範例的資訊,請參閱
<關於圖像處理範例>。
1. 定義大小為 N x P 的矩陣 M。
2. 餘弦轉換的實行使用類型 II DCT。定義 DCT 作為此轉換的分析公式。
3. 計算矩陣 DCT。
4. 將函數 dct 套用至矩陣 M。
5. 計算 DCT 與 dct 函數之間的最大誤差。
能量壓縮
餘弦轉換具有非常好的能量壓縮屬性,換言之,該轉換會集中在轉換的前幾個係數之大部份的能量。
1. 定義輸入矩陣。
2. 將 dct函數套用至矩陣 M,並加以計算。
所得出的矩陣顯示與係數值相關的大部份能量,且會集中在前幾個元素。
idct
反函數係用於從原始圖像的轉換恢復原始圖像。
1. 讀取黑白版的蒙娜麗莎。
(mona.bmp)
2. 套用 dct 函數轉換圖像。
(mona_noise.bmp)
3. 套用反函數以恢復圖像。
(mona_rec.bmp)
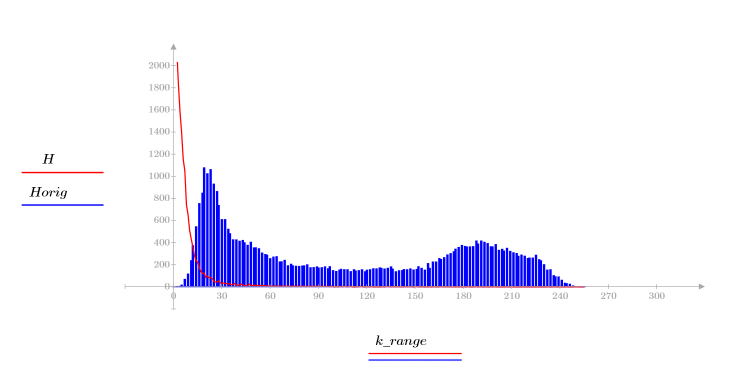
4. 檢視轉換圖像與原始圖像的柱狀圖,以核對 DCT 的能量壓縮屬性。
轉換圖像會將大部份能量集中在柱狀圖的前幾個柱狀中,而原始圖像的分佈則會散開。這使得轉換圖像更適合於編碼或傳輸,因為大部份的圖像資訊透過非常少的頻率元件即可轉送。因此會使用 DCT 壓縮圖像。