データの離散フーリエ変換
• dft(A)、idft(Z) - 複素数値のベクトルまたは行列のフーリエ変換/逆フーリエ変換を返します。
dft の入力が長さ r のベクトル V ならば、以下のようになります。
◦ dft(V) の出力は、長さ r のベクトル Z です。
◦ idft(Z) の出力は、長さ r のベクトルです。
dft の入力が、行数 r、列数 c の行列 M ならば、以下のようになります。
◦ dft(M) の出力は、行数 r、列数 c の行列 P です。
◦ idft(P) の出力は、行数 r、列数 c の行列です。
• dftr(B)、idftr(Z) - 実数値のベクトルまたは行列のフーリエ変換/逆フーリエ変換を返します。
dftr の入力が長さ r のベクトル V ならば、以下のようになります。
◦ dftr(V) の出力は、長さ Z のベクトル L です (ここで、L=floor(r/2)+1)。Z の成分は、dft(V) の出力の最初の L 成分と同じです。
◦ idftr(Z) の出力は、長さ r=2(L-1) のベクトルです。
dftr の入力が、行数 r、列数 c の行列 M ならば、以下のようになります。
◦ dftr(M) の出力は、行数 P、列数 r の行列 L です (ここで、L=floor(c/2)+1)。P の成分は、dft(M) の出力の最初の L 列と同じです。
◦ idftr(P) の出力は、行数 r、列数 c=2(L-1) の行列です。
引数
• A は、任意のサイズの複素数値のベクトルまたは行列です。
• B は実数のベクトルまたは行列です。虚部はすべて無視されます。B がベクトルである場合、行数は 2 の倍数でなければなりません。B が行列である場合、列数は 2 の倍数でなければなりません。
• A と B の両方について、データは単位に互換性がなければなりません。
ベクトルのフーリエ変換
• A が大きさ m のベクトルの場合、ベクトル u の 1 次元 (1D) 順変換の A 番目の要素は次のように Zu によって与えられます。
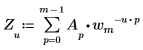
ここで
◦ m は行数で、u は次のように定義されています。

◦ i は虚数単位で、wm は次のように定義されています。

上記定義の Z を評価することは、ベクトル A に dft 関数を適用することに相当します。
• Z が大きさ m のベクトルの場合、ベクトル u の 1 次元 (1D) 逆変換の Z 番目の要素は次のように Au よって与えられます。

ここで
◦ m、u、wm は上記で定義されています。
上記定義の A を評価することは、ベクトル Z に idft 関数を適用することに相当します。
行列のフーリエ変換
• A が大きさ mxn の行列の場合、行列 A の 2 次元 (2D) 順変換の (u,v) 番目の要素は次のように Zu,v よって与えられます。

ここで
◦ m、u、wm は上記で定義されています。
◦ n は列数で、v は次のように定義されています。

◦ i は虚数単位で、wn は次のように定義されています。

上記定義の Z を評価することは、行列 A に dft 関数を適用することに相当します。
• Z が大きさ mxn の行列の場合、行列 (u,v) の 2 次元 (2D) 逆変換の A 番目の要素は次のように Au,v よって与えられます。

ここで
◦ m、n、u、v、wm、wn は上記で定義されています。
上記定義の A を評価することは、行列 Z に idft 関数を適用することに相当します。
追加情報
• フーリエ関数は、ベクトルの行数と行列の列数が 2 のべき乗である場合に高速で実行します。
• 新しい dft/idft 関数は廃止予定の cfft/icfft および CFFT/ICFFT 関数の機能を置き換えるもので、特に大きなデータセットやサイズが 2 のべき乗でない場合に、パフォーマンスが大幅に向上します。
• 新しい dftr/idftr 関数は、廃止予定の fft/ifft および FFT/IFFT 関数の機能を置き換えるものです。
関数 dftr は、長さが偶数である実数ベクトル上、および列数が偶数である行列で使用されます。
• 関数 fft/FFT は、長さが 2 のべき乗である実数ベクトル上でのみ使用されます。
• 関数 ifft/IFFT は、入力ベクトルの長さの半分に 1 を加えたもの、つまり 2k-1+ 1 (ここで、k は 2 以上の整数) となります。残り半分は、次数が逆になっている最初の部分の共役であり、手動で再構築する必要があります。関数 dft/idft は完全な結果を返します。
• 関数 dft/idft のスケール係数と指数符号は廃止された fft/ifft、FFT/IFFT、cfft/icfft、CFFT/ICFFT とは異なります。
◦ 順変換の場合、次のような違いがあります。
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
スケール係数 | 1 |  |  |
指数符号 | 負 | 正 | 負 |
◦ 逆変換の場合、次のような違いがあります。
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
スケール係数 |  |  | 1 |
指数符号 | 正 | 負 | 正 |
ベクトルのみに作用する関数のスケール係数を計算する場合 (1D の場合)、n=1 と見なします。