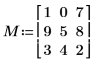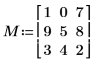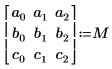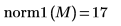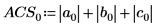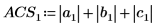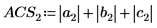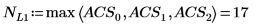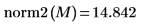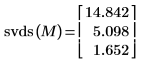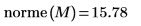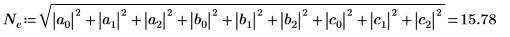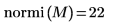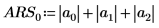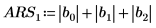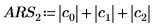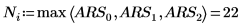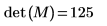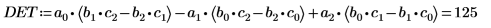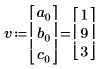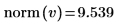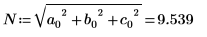Ejemplo: funciones de norma y determinante de la matriz
1. Defina una matriz cuadrada.
2. Defina los elementos de la matriz en nombres de variables genéricos.
3. Utilice la función norm1 para buscar la norma L1 de la matriz M.
De forma alternativa, busque la norma L1 calculando el valor máximo de las sumas absolutas de las columnas de M.
4. Utilice la función norm2 para buscar la norma L2 de la matriz M.
De forma alternativa, utilice la función svds para buscar el valor singular absoluto más alto de la matriz M.
La función svds devuelve un vector de valores singulares ordenados, por lo que el valor superior es el valor singular más alto de la matriz M.
5. Utilice la función norme para buscar la norma euclídea de la matriz M.
De forma alternativa, calcule manualmente la raíz cuadrada de la suma de los cuadrados absolutos de la matriz M.
6. Utilice la función normi para buscar la norma infinita de la matriz M.
De forma alternativa, utilice la función max para calcular manualmente el valor máximo de las sumas absolutas de las filas de la matriz M.
7. Utilice la función det para buscar el determinante de la matriz M.
De forma alternativa, calcule manualmente el determinante de la matriz M.
8. Utilice la función norm para buscar la norma de un vector que contenga los elementos de la columna 0 de la matriz M.
De forma alternativa, calcule manualmente la norma del vector v.