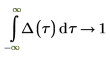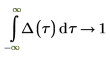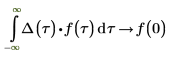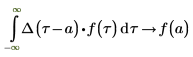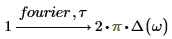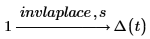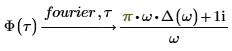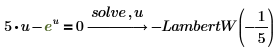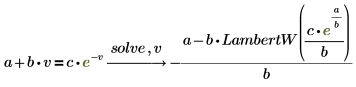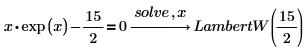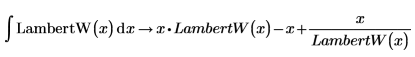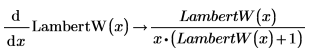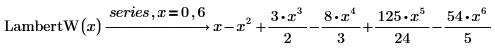Beispiel: Delta-Funktion von Dirac (Delta-Distribution) und LambertW-Funktion
Dieses Beispiel enthält Informationen über die Eigenschaften der Delta-Funktion von Dirac und der LambertW-Funktion.
Die Delta-Funktion von Dirac
Die Delta-Funktion von Dirac hat die folgenden Eigenschaften:
Zurückgegebene Ergebnisse werden durch Folgendes in Bezug auf Dirac Delta transformiert:
Im oben genannten Beispiel ist Φ die Heaviside-Sprungfunktion.
Die LambertW-Funktion
Die LambertW-Funktion ist in der symbolischen Lösung folgender Gleichungen enthalten:
Dies sind das Integral, die Ableitung und die Taylor-Reihenentwicklungserweiterung der Funktion LambertW: