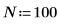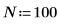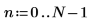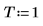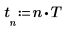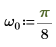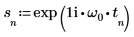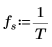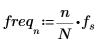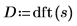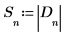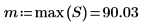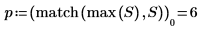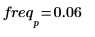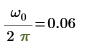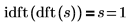Beispiel: DFT von komplexen Funktionen
Verwenden Sie die Funktionen dft und idft, um die komplexe oder reelle Fourier-Transformation bzw. die inverse Fourier-Transformation zu berechnen.
1. Erstellen Sie einige simulierte komplexe Daten mit N Datenpunkten.
2. Definieren Sie den Stichprobenabstand.
3. Verwenden Sie die Funktion exp, um das folgende Signal zu definieren.
4. Definieren Sie die Abtastfrequenz und die Frequenz, die dem n-ten Eintrag im transformierten Vektor entspricht.
5. Wenden Sie die Funktion dft an, um die Daten in den Frequenzbereich zu transformieren.
6. Speichern Sie den Betrag der Elemente von Array D in einem neuen Array.
7. Berechnen Sie mit den Funktionen match und max die Amplitude und die Frequenz des Spitzenwerts.
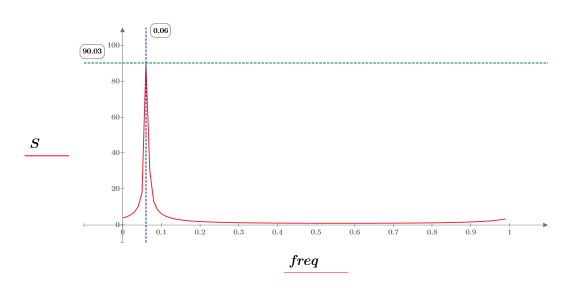
8. Stellen Sie den Betrag von DFT als Frequenzfunktion dar.
9. Zeigen Sie, dass die Frequenz des Spitzenwerts ω0/2π entspricht.
10. Zeigen Sie unter Verwendung der Funktion idft, dass die IDFT einer DFT eines Signals das Signal selbst liefert.