|
Type d'analyse :
|
Réponse dynamique transitoire
|
|
Type de modèle :
|
3D
|
|
Comparaison :
|
ANSYS n° 74
|
|
Référence :
|
Thomson, W.T. Vibration Theory and Applications. NJ: Prentice-Hall, Inc. 2nd printing, 1965. p. 99, Article 4.1.
|
|
Description :
|
Un système à ressort de masse est soumis à une charge d'impact, puis subit une vibration libre. Déterminez le déplacement au temps t = 0.1 s pour un système avec amortisseur et un système sans amortisseur.
|

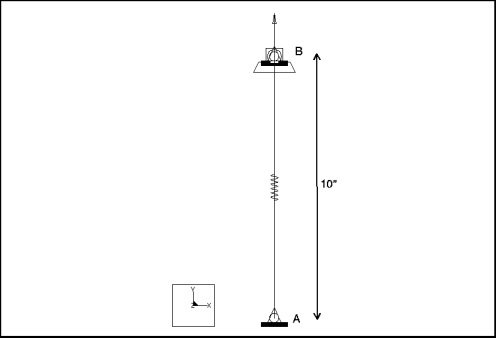
Type d'élément : | masse (1), ressort (1) | ||
Unités : | IPS | ||
Cotes : | longueur de ressort : 10 (arbitraire) | ||
Propriétés massiques : | |||
M : 0,5 | Mxx : 0 | Mxy : 0 | Mxz : 0 |
Myy : 0 | Myz : 0 | Mzz : 0 | |
Propriétés de ressort : (raideur en traction) | |||
Kxx : 200 | Kxy : 0 | Kxz : 0 | |
Kyy : 0 | Kyz : 0 | Kzz : 0 | |
Restrictions : | placé sur le point A : fixe dans l'ensemble des DDL placé sur le point B : fixe dans tous les DDL sauf TransY | ||
Charges : | placé sur le point B : FY = 10 Distribution : N/D Variation spatiale : N/D | ||
Théorie | ANSYS | Structure1 | % de différence | |
Déplacement max. à t = 0.1 (a=undamped) | 0,909297 | 0,90693 | 0,909297 | 0,0 % |
Déplacement max. à t = 0.1 (a=damped, damping=70%) | 0,3418 | 0,34252 | 0,3418 | 0,0 % |
% de convergence : 0,0 % sur fréquence | P max. : N/D | Nbre d'équations : 1 | ||