|
Type d'analyse :
|
Réponse dynamique au choc
|
|
Type de modèle :
|
3D
|
|
Comparaison :
|
ANSYS n° 70
|
|
Référence :
|
Biggs, J. M. Introduction to Structural Dynamics. McGraw-Hill Book Co., New York, 1964.
|
|
Description :
|
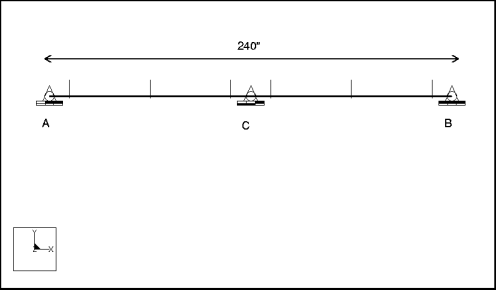
Une poutre simplement supportée est soumise à un déplacement vertical des deux supports. Le mouvement est défini en termes de spectre de réponse de déplacement sismique. Déterminez le déplacement maximal, de même que la contrainte de flexion maximale.
|

Type d'élément : | poutre (2) | ||
Unités : | IPS | ||
Cotes : | longueur : 240 hauteur : 14 | ||
Propriétés des poutres : | Aire : 273,9726 IYY : 333,333 Cisaillement FY : 0,83333 CY : 7 | J : N/D IZZ : 333,333 Cisaillement FZ : 0,83333 CZ : 7 | |
Propriétés des matériaux : | Masse volumique : 0,00073 Coût par unité de masse : 0 Module de Young :3e7 | Coefficient de Poisson : 0,3 Dilatation thermique : 0 Conductivité : 0 | |
Restrictions : | Emplacement : | Degrés de liberté : | |
restriction1 | placé sur le point A | fixe dans TransY et TransZ | |
placé sur le point B | fixe dans TransX, TransY et TransZ | ||
placé sur le point C | fixe dans TransZ, RotX et RotY | ||
Spectre de réponse : | Fréquence : | Déplacement : | |
resp_spectrum1 | 0 10 | 0,44 0,44 | |
Théorie | ANSYS | Structure | % de différence | |
Fréquence (Frequency) | 6,0979 | 6,0974 | 6,0953 | 0,04 % |
Déplacement max. (m=disp_max) | 0,560 | 0,553 | 0,560 | 0 % |
Contrainte de flexion max. | 20158 | 20156 | 20138 | 0,1 % |
% de convergence : 0,0 % sur fréquence | P max. : 6 | Nbre d'équations : 70 | ||