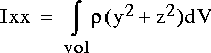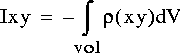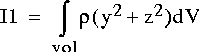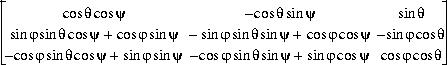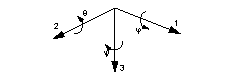About Computing Mass Properties
You can set the default mass units for all new parts and assemblies that you create using the pro_unit_mass configuration option.
Mass properties for a part or assembly is calculated using system parameters within a relation. However, mass properties are not automatically updated when the model changes. You must recalculate the mass properties to see the effect of model changes.
|
|
 In Welding assemblies, you can include or exclude welds from the mass properties calculation. Mass property calculations for light welds are approximate, unless you specify weld section references. Set the add_weld_mp configuration option to yes to include welds in the mass properties calculation. The default is no. |
If dimension bounds have been set, mass property calculations are based on hypothetical dimension values.
If features are suppressed, the mass properties are calculated as if the features did not exist. If a part has been simplified for assembly purposes and contains many suppressed features, mass properties may be assigned to the part so that those values are used in calculating mass properties of an assembly.
If parts on layers have been blanked from the current view, they are still used to calculate the mass properties of an assembly. Blanking items only affects the display of the object, not its composition.
The computed mass properties for a part or assembly include:
• Volume—Total volume of the model
• Surface area—Total surface area of the model
• Density—For part mass properties, the specified part density is listed here.
For assembly mass properties, the average density of its components is listed. The average density is calculated as the total mass divided by the total volume:
Average density=(total mass of assembly)/(total volume of assembly)
The density of each individual part is used in the calculation of the mass properties.
• Mass—Total mass of the model
• Center of gravity—Location of the center of gravity with respect to a specified coordinate system. The center of gravity and coordinate system are displayed graphically on the model.
• Inertia tensor at the specified coordinate system origin and axes. The values are computed as follows:
-and so forth.
-and so forth
-where p = specified part density.
• Inertia tensor at the center of gravity and oriented along the specified coordinate system axes
• Principal moments of inertia—Moments of inertia at the center of gravity with respect to the principal axes
The principal coordinate axes, which define a new coordinate system, are labeled 1, 2, 3 instead of x, y, z. In the preceding equation, y is the coordinate along the principal axis 2 and z is the coordinate along the principal axis 3.
• Rotation matrix and rotation angles—Rotation from the coordinate axes to the principal axes in matrix and angular form. Rotation matrix is computed as follows:
-where φ is the rotation angle about the 1 axis, θ is the rotation angle about the 2 axis, and ψ is the rotation angle about the 3 axis.
Rotation Angles
• Radii of gyration—The radii of gyration at the center of gravity with respect to the principal axes
• For an assembly, a summary of the mass properties of its components