Creo Flow Analysis > Postproceso > Definición de las especificaciones físicas > Turbulencia > Física > Modelos de turbulencia
  
Modelos de turbulencia
Se puede calcular la viscosidad turbulenta efectiva en un sistema de fluidos según el modelo de viscosidad de remolino. Existen dos modelos en el modelo de viscosidad de remolino:
• Modelo k-épsilon estándar
El modelo k-épsilon estándar es un modelo de Turbulencia (Turbulence) disponible en Creo Flow Analysis.
La formulación para la energía cinética turbulenta k es:
La formulación para la velocidad de disipación turbulenta ε es:
donde,
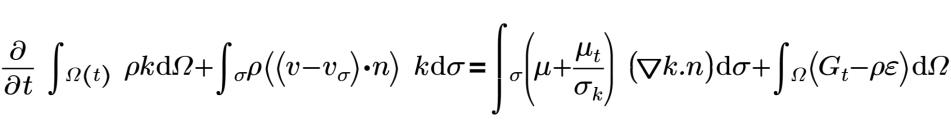
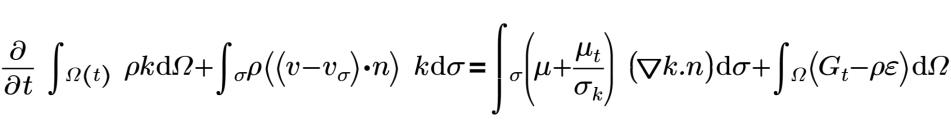
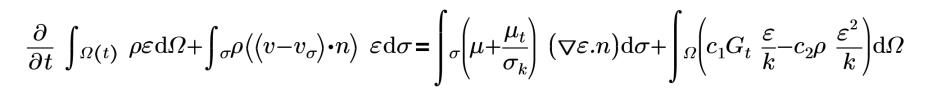
c1=1.44
constantes C1
c2=1.92
constantes C2
σk=1
número de Prandtl de energía cinética de turbulencia
σz=1
número de Prandtl de velocidad de disipación de turbulencia
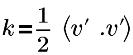energía cinética turbulenta
v’
velocidad de fluctuación turbulenta
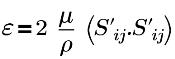velocidad de disipación de energía turbulenta
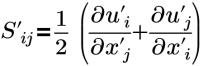tensor de deformación
u’i(i=1,2,3)
componentes de la velocidad de fluctuación turbulenta
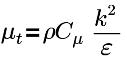viscosidad turbulenta, con Cμ=0.09 y E=9.793
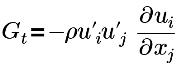término de generación de turbulencia
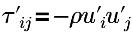tensión de Reynolds de turbulencia
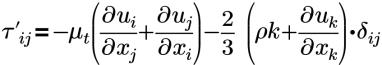la aproximación de Boussinesq a la tensión de Reynolds
Referencias: Launder, B.E. & Spalding, D.B. (1974) "The numerical computation of turbulent flows", Computer Methods, Applied Mechanics and Engineering, vol. 3, p. 269-289
• Modelo k-épsilon de grupo de renormalización (RNG)
El modelo k-épsilon de grupo de renormalización (RNG) es un modelo de Turbulencia (Turbulence) disponible en Creo Flow Analysis. Este modelo es parecido al modelo k-épsilon estándar, pero con una expresión que implica dos nuevas constantes que se utilizan para modificar el término RNG C2 en la siguiente ecuación:
donde,
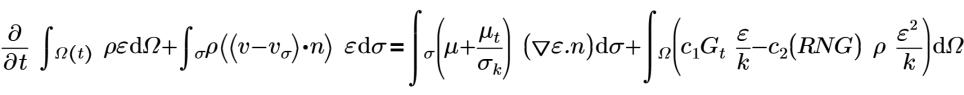
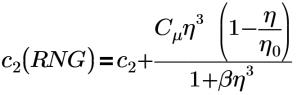
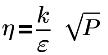
η0=4.38
Constante RNG (constante codificada de forma fija en Flow Analysis)
β=1.92
Constante RNG (constante codificada de forma fija en Flow Analysis)
P
presión local
c1=1.44
constantes C1
c2=1.92
constantes C2
σk=1
número de Prandtl de energía cinética de turbulencia
σz=1
número de Prandtl de velocidad de disipación de turbulencia
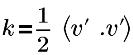energía cinética turbulenta
v’
velocidad de fluctuación turbulenta
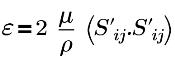velocidad de disipación de energía turbulenta
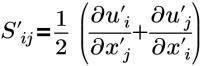tensor de deformación
u’i(i=1,2,3)
componentes de la velocidad de fluctuación turbulenta
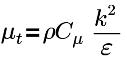viscosidad turbulenta, con Cμ=0.09
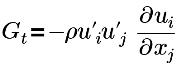término de generación de turbulencia
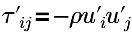tensión de Reynolds de turbulencia
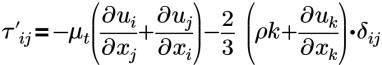aproximación de Boussinesq a la tensión de Reynolds
Referencias: Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, p. 1510-1520