Анализ потока Creo > Предварительная обработка > Определение физики > Турбулентность > Физика > Модели турбуленции
  
Модели турбуленции
Можно вычислить эффективную турбулентную вязкость в жидкостной системе на основе модели вязкости вихря. Для модели вязкости вихря имеется две модели.
• Стандартная модель к-эпсилон
Стандартная модель к-эпсилон - это модель Турбуленции (Turbulence), доступная в анализе потоков Creo.
Формула для кинетической энергии турбуленции k:
Формула для интенсивности рассеивания турбуленции ε:
где
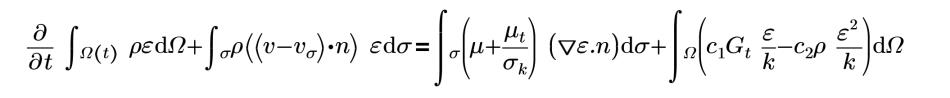
c1=1.44
константы C1
c2=1.92
константы C2
σk=1
Число Прандтля для кинетической энергии турбуленции
σz=1
Число Прандтля для интенсивности рассеивания турбуленции
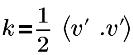Кинетическая энергия турбуленции
v’
Скорость турбулентных флуктуаций
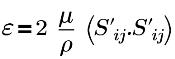Интенсивность рассеивания энергии турбуленции
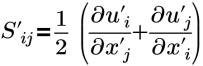Тензор напряжений
u’i(i=1,2,3)
Компоненты скорости турбулентных флуктуаций
турбулентная вязкость, с Cμ=0.09 и E=9.793
Выражение генерации турбуленции
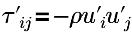Турбулентное напряжение Рейнольдса
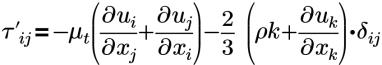Приближение Буссинеска для напряжения Рейнольдса
См.: Launder, B.E. & Spalding, D.B. (1974) “The numerical computation of turbulent flows,” Computer Methods, Applied Mechanics and Engineering, том 3, стр. 269-289)
• Модель к-эпсилон для ренормализационной группы (RNG)
Модель к-эпсилон для ренормализационной группы (RNG) - это модель Турбуленции (Turbulence), доступная в анализе потоков Creo. Эта модель аналогична стандартной модели к-эпсилон, но с выражением, включающим две новые константы, которые используются, чтобы изменить элемент C2 RNG в приведенном ниже уравнении:
где
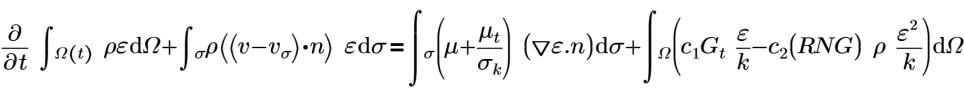
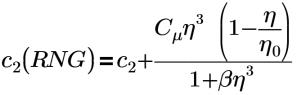
η0=4.38
Константа RNG (встроенная константа в модуле анализа потоков)
β=1.92
Константа RNG (встроенная константа в модуле анализа потоков)
P
Локальное давление
c1=1.44
константы C1
c2=1.92
константы C2
σk=1
Число Прандтля для кинетической энергии турбуленции
σz=1
Число Прандтля для интенсивности рассеивания турбуленции
Кинетическая энергия турбуленции
v’
Скорость турбулентных флуктуаций
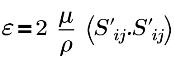Интенсивность рассеивания энергии турбуленции
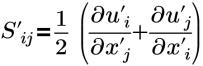Тензор напряжений
u’i(i=1,2,3)
Компоненты скорости турбулентных флуктуаций
турбулентная вязкость, с Cμ=0.09
Выражение генерации турбуленции
Турбулентное напряжение Рейнольдса
Приближение Буссинеска для напряжения Рейнольдса
См.: Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, том 4, № 7, стр. 1510-1520