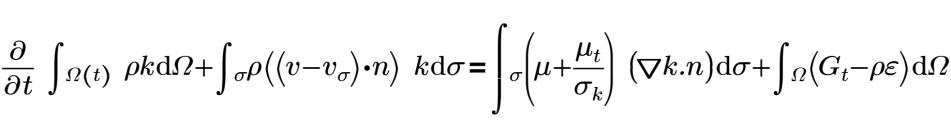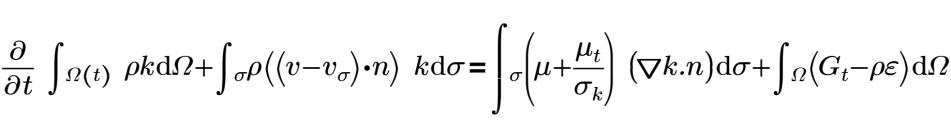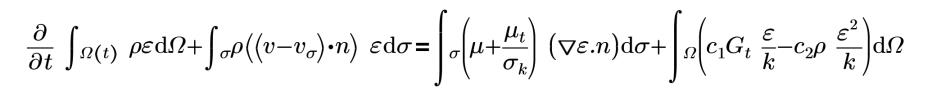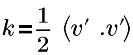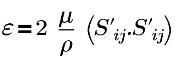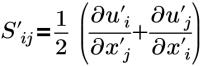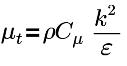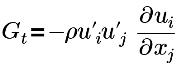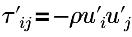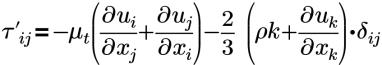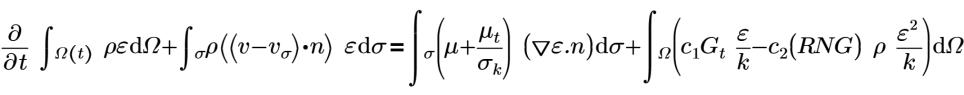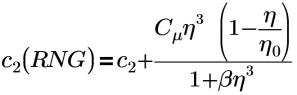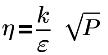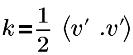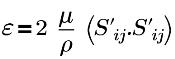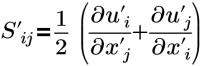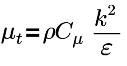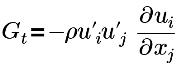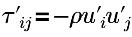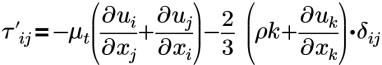터뷸런스 모델
유체 시스템에서 와동 점도 모델에 따라 유효
터뷸런스 점도를 계산할 수 있습니다. 와동 점도 모델에는 다음과 같은 두 가지 모델이 있습니다.
• 표준 K-엡실론 모델
표준 K-엡실론 모델은 Creo Flow Analysis에서 사용할 수 있는 터뷸런스(Turbulence) 모델입니다.
여기서 각 항목은 다음을 나타냅니다.
c1=1.44 | 상수 C1 |
c2=1.92 | 상수 C2 |
σk=1 | 터뷸런스 운동 에너지 프란틀 수 |
σz=1 | 터뷸런스 소산율 프란틀 수 |
| 터뷸런스 운동 에너지 |
v’ | 터뷸런스 변동 속도 |
| 터뷸런스 에너지 소산율 |
| 변형 텐서 |
u’i(i=1,2,3) | 터뷸런스 변동 속도의 컴포넌트 |
| 터뷸런스 점도, Cμ=0.09 및 E=9.793 |
| 터뷸런스 생성 항 |
| 터뷸런스 레이놀즈 응력 |
| 레이놀즈 응력에 대한 부씨네스크 근사 |
참조: Launder, B.E. & Spalding, D.B. (1974) "The numerical computation of turbulent flows," Computer Methods, Applied Mechanics and Engineering, vol. 3, pp. 269-289
• RNG(재규격화 그룹) K-엡실론 모델
RNG(재규격화 그룹) K-엡실론 모델은 Creo Flow Analysis에서 사용할 수 있는 터뷸런스(Turbulence) 모델입니다. 이 모델은 표준 K-엡실론 모델과 유사하지만, 아래 방정식에서 C2 RNG 항을 수정하는 데 사용되는 두 개의 새로운 상수가 포함된 식이 있습니다.
여기서 각 항목은 다음을 나타냅니다.
η0=4.38 | RNG 상수(Flow Analysis에서 하드 코딩된 상수) |
β=1.92 | RNG 상수(Flow Analysis에서 하드 코딩된 상수) |
P | 로컬 압력 |
c1=1.44 | 상수 C1 |
c2=1.92 | 상수 C2 |
σk=1 | 터뷸런스 운동 에너지 프란틀 수 |
σz=1 | 터뷸런스 소산율 프란틀 수 |
| 터뷸런스 운동 에너지 |
v’ | 터뷸런스 변동 속도 |
| 터뷸런스 에너지 소산율 |
| 변형 텐서 |
u’i(i=1,2,3) | 터뷸런스 변동 속도의 컴포넌트 |
| 터뷸런스 점도, Cμ=0.09 |
| 터뷸런스 생성 항 |
| 터뷸런스 레이놀즈 응력 |
| 레이놀즈 응력에 대한 부씨네스크 근사 |
참조: Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, pp1510-1520