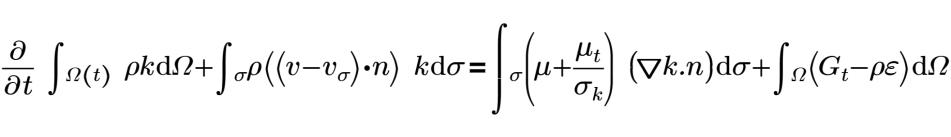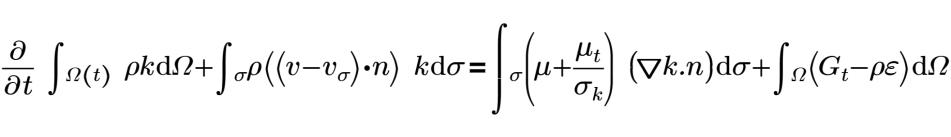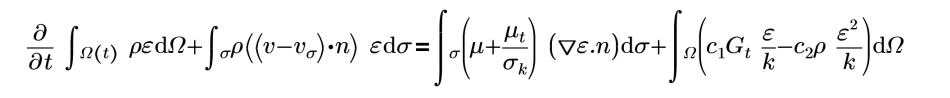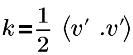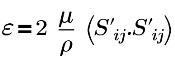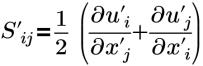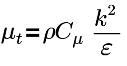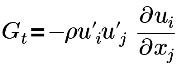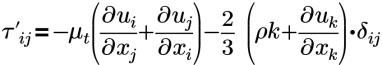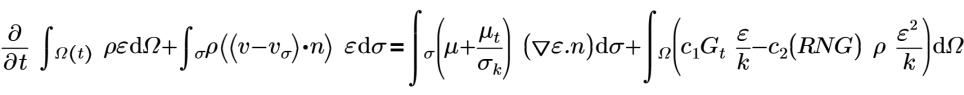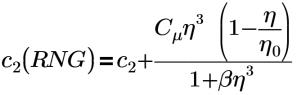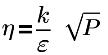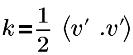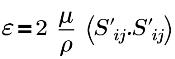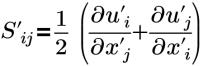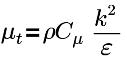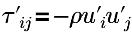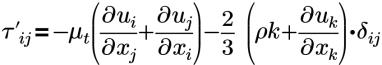湍流模型
您可以在基于涡黏度模型的流体系统中计算有效的
湍流黏度。涡黏度模型中包含两个模型:
• 标准 K-Epsilon 模型
标准 K-Epsilon 模型为可在 Creo Flow Analysis 中使用的“湍流”(Turbulence) 模型。
其中,
c1=1.44 | 常量 C1 |
c2=1.92 | 常量 C2 |
Σk= 1 | 湍流动能普朗特数 |
σz=1 | 湍流耗散率普朗特数 |
| 湍流动能 |
v’ | 湍流波动速度 |
| 湍流能量耗散率 |
| 应变张量 |
u’i(i=1,2,3) | 湍流波动速度的分量 |
| 扰动黏度,其中 Cμ=0.09,E=9.793 |
| 湍流生成项 |
| 湍流雷诺应力 |
| 与雷诺应力近似的 Boussinesq |
参考文献:Launder, B.E. & Spalding, D.B. (1974) “The numerical computation of turbulent flows,” Computer Methods, Applied Mechanics and Engineering, vol. 3, pp. 269-289
• 重整化群 (RNG) K-Epsilon 模型
重整化群 (RNG) K-Epsilon 模型为可在 Creo Flow Analysis 中使用的“湍流”(Turbulence) 模型。该模型与标准 K-Epsilon 模型相似,但是其表达式包含两个新常量,用于修正以下方程中的 C2 RNG 项:
其中,
η0=4.38 | RNG 常量 (Flow Analysis 中的硬编码常量) |
β=1.92 | RNG 常量 (Flow Analysis 中的硬编码常量) |
P | 局部压力 |
c1=1.44 | 常量 C1 |
c2=1.92 | 常量 C2 |
Σk= 1 | 湍流动能普朗特数 |
σz=1 | 湍流耗散率普朗特数 |
| 湍流动能 |
v’ | 湍流波动速度 |
| 湍流能量耗散率 |
| 应变张量 |
u’i(i=1,2,3) | 湍流波动速度的分量 |
| 扰动黏度,其中 Cμ=0.09 |
| 湍流生成项 |
| 湍流雷诺应力 |
| 与雷诺应力近似的 Boussinesq |
参考文献:Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, pp1510-1520